Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 54
Calcule a integral trocando a ordem de integração.
Passo 1
E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos lá!
Vamos resolver essa integral trocando a ordem de integração. Antes de começarmos, precisamos entender a região de integração e como ela é delimitada. Isso é importante para que possamos visualizar a área correta e fazer a mudança de variáveis com precisão.
Primeiro, vamos identificar e esboçar a região de integração:
O primeiro passo é esboçar a região de integração:
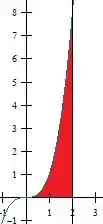
A curva é inversa da função , que é uma parábola de abertura para a direita. E a reta é uma linha vertical.
As interseções dessas curvas no plano delimitam a região de integração. Agora, vamos mudar a ordem de integração.
Passo 2
Para trocar a ordem de integração, vamos reescrever os limites de em função de :
- Inicialmente, varia de até . Na nova ordem, variará de até .
- varia de até . Na nova ordem, variará de até .
Então, a integral de torna:
Passo 3
Agora que temos a integral com a ordem de integração trocada, vamos resolvê-la. Primeiro, integramos em :
Fazendo , temos que . Assim, quando , e quando , . Substituindo na integral, temos:
Integrando :