Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 47
Esboce a região de integração e mude a ordem de integração.
Passo 1
E aí, galerinha! Tudo show?
A questão pede para traçamos a região de integração de:
A região de integração de uma integral dupla é justamente de onde obtemos os limites de integração, então para encontrar essa região , nós vamos partir dos intervalos de derivação, que são:
É possível observar que estamos trabalhando com uma região do tipo , pois estamos integrando inicialmente em . Para mudar a ordem de integração, vamos precisar expressar a região que vamos ter esboçado como uma região do tipo II.
Vem ver como fica!
Passo 2
Agora que determinamos a nossa região, podemos esboça-la. Portanto:
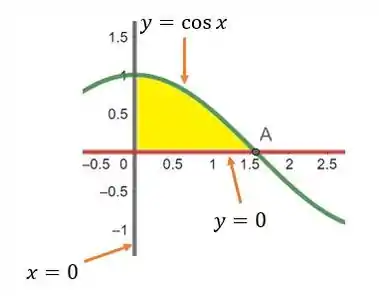
Passo 3
Agora que esboçamos a região de integração, vamos mudar sua ordem de integração.
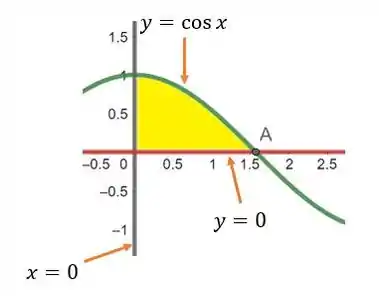
Vamos pensar que agora é uma região do tipo II, onde está entre dois valores constantes e está entre duas funções, que é o contrário da abordagem que fizemos no passo acima.
Sabemos que a região é limitada inferiormente pela reta e superiormente por . Para os limites laterais temos, à esquerda e à direita. Portanto:
Agora é a integral em relação a que tem limites de integração com variável, por isso mudamos a ordem e nosso agora é a integral “de dentro”.