Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 40
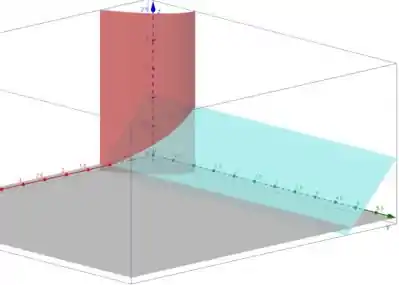
Esboce o sólido cujo volume é dado pela integral iterada.
Passo 1
E aí, pessoal! Tudo certo?
Vamos entender o que nossa questão pede. Ela nos dá a integral dupla:
E quer que a gente esboce o volume que essa integral está descrevendo. Isso é um gráfico de um sólido e vamos precisar usar um software para gerar esse gráfico, como o Geogebra.
Primeiro, vamos usar os limites de integração da nossa integral para entender em qual região no plano essa integral está sendo calculada, e plotar o gráfico dessa região.
Depois vamos olhar o integrando, que vai ser a função:
que vai delimitar nosso volume, já que a integral dupla de uma função é o cálculo do sólido abaixo dela na região .
Vamos lá!
Passo 2
A questão deu a integral e pede para você achar o sólido cujo volume é dado por essa integral. Vamos olhar primeiro para o domínio de integração. Enquanto varia de até , varia da reta até . Assim, o domínio é representado por:
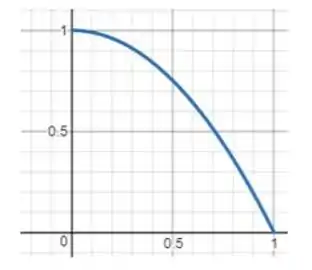
Passo 3
Agora vamos olhar para o integrando. Podemos encarar
como a tampa superior do sólido, já que a integral dupla de uma função é justamente o volume abaixo do gráfico dessa função e acima do plano , que é onde se encontra a região .
Logo, a tampa inferior será . Assim o sólido pode ser descrito por:
Trata-se de um sólido delimitado no primeiro octante, abaixo do plano e dentro do cilindro parabólico .:
