Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 44
Represente graficamente o sólido que se encontra entre a superfície e o plano e é limitada pelos planos , , e . Então encontre o volume.
Passo 1
Belê, pessoal? Vamos analisar essa questão.
Ela quer o gráfico do sólido entre uma superfície e um plano , e que também limitado por outros planos, esses aqui ó:
Depois disso, pede o volume do sólido.
Show!
Para plotar o sólido podemos usar o Maple e inserir os parâmetros que estão no enunciado. Geramos isso:
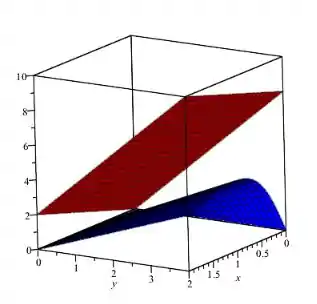
Podemos notar que a função é o limite superior da região (o nosso plano em vermelho!) e é o limite inferior (nossa superfície em azul).
Portanto:
Limitado pelo retângulo:
Ou seja, aqueles outros valores, que limitavam a região do sólido representado, são nossos limites de integração.
Passo 2
O volume encontramos a partir de:
Substituindo pelo que descobrimos:
Resolvendo de dentro para fora, temos:
Colocando nossos limites de integração:
Passo 3
Vamos calcular a integral de fora:
Resolvendo:
Inserindo também os limites de integração: