Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.5 - Ex. 4
Encontre a área da superfície.
A parte do plano que cruza acima do triangulo com vértices e.
Passo 1
Fala, pessoal! Cês tão bem?
A questão pede pra gente achar a área da superfície do plano:
que cruza acima do triangulo com vértices e.
A área da superfície com a equação é:
Ou seja, vamos achar as derivadas parciais de e da função:
- : derivada da nossa função em relação a , onde tratamos as outras variáveis como constantes.
- : derivada da nossa função em relação a , onde tratamos as outras variáveis como constantes.
- Vemos que os valores de variam entre 0 e 2.
- Vemos que os valores de variam entre o eixo e uma reta que passa pela origem e a coordenada em é duas vezes a coordenada em :
E também vamos precisar dos limites de integração da função que é dado pela região no plano . Para ter nossa interseção da nossa função com o plano é só igualarmos na nossa equação.
Lembrando também que:
Depois de acharmos as derivadas parciais e os limites de integração, é só a gente resolver a integral dupla daquele jeito que sabemos, começando pela integral “de dentro”.
Vamos lá!
Passo 2
Temos então que encontrar as derivadas parciais e . Temos que:
portanto:
Como a derivada de é e os outros termos são considerados constantes (derivada da constante é zero), vamos ter:
Como a derivada de é e os outros termos são considerados constantes (derivada da constante é zero), vamos ter:
Substituindo as derivadas parciais na nossa integral, a área será:
A área será:
Somando os termos:
Passo 3
Nossa região no plano é descrita por:
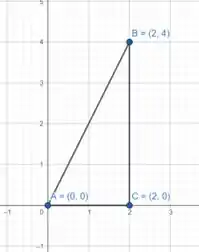
o triangulo com vértices e
Para aplicar os limites, temos que achar os valores máximos e mínimos para cada variável:
Então os limites são:
Então, nossos limites de integração serão:
Passo 2
Ufa! Agora que nossa integral está completa, é só a gente resolver! Resolvendo, temos que começar pela integral de dentro em relação a , considerando como constante:
Aplicando os limites de integração:
Para resolver, temos que aplicar o método da substituição, onde vamos chamar uma parte da nossa função de . Temos que:
Logo sua derivada será:
Quando temos que e quando , portanto:
Tirando a raiz quadrada do numerador e do denominador:
Resolvendo a integral:
E aplicando os limites de integração:
Simplificando, teremos por fim: