Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 33
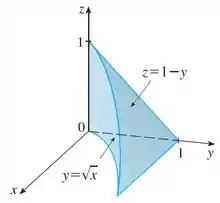
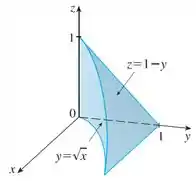
A figura mostra a região de integração da integral
Reescreva essa integral como uma integral iterada equivalente nas cinco outras ordens.
Passo 1
E aí, pessoal! Tudo beleza?
A questão pede pra gente reescrever nossa integral:
Em 5 outras ordens.
As ordens de integração mudam conforme mudamos a ordem de cada fator:
Como temos que manter sempre “pra dentro” as variáveis que tem funções nos limites de integração, vamos sempre encontrar formas diferentes em cada integral para descrever nossa região dada na imagem do enunciado, conforme cada ordem de integração que estamos considerando.
Vamos lá!
Passo 2
O enunciado já nos deu uma ordem de integração:
Daí tiramos que:
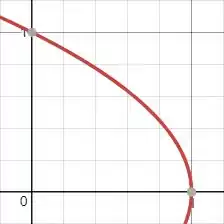
Pela analise do gráfico do plano podemos colocar entre duas constantes e entre duas funções. Então temos aqui que:
E, escrevendo:
Em função de , elevamos a equação ao quadrado e ficamos com:
Mantemos o mesmo e ficamos com:
Pronto! Primeira forma das 5 que precisamos achar.
Passo 3
Podemos também colocar na integral mais interna a variação de da seguinte forma
e a variação das outras variáveis, vai sair da intersecção entre e
No plano temos
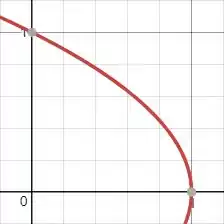
Ou
E podemos ter mais duas formas diferentes de escrevermos nossa integral do enunciado:
Passo 4
E se colocarmos entre funções de e temos a variação
enquanto as outras variáveis variam de ao plano e temos:
E ficamos com mais duas formas de escrever nossa integral inicial, totalizando 5!