Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.7 - Ex. 28
Esboce o sólido cujo volume é dado pela integral iterada.
Passo 1
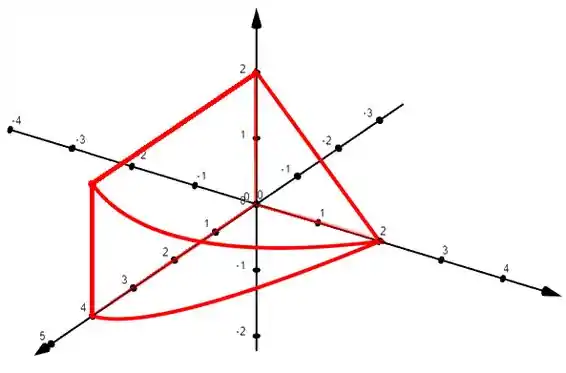
Vamos lá pessoal, precisamos eboçar um sólido que o volume é:
E como vamos fazer isso? Ora, perceba que se vamos esboçar um sólido, então certamente precisaremos fazer um desenho. Para isso, recomendo que já construa os 3 eixos e , e constra nesses eixos as separações de unidade. Após isso só precisamos identificar quais são os pontos que temos que marcar e qual o comportamento de cada curva que conecta esses pontos.
Passo 2
Como temos uma integral do tipo
Então precisamos saber o que é , pelas variações temos
Só precisamos ter uma noção de como são o plano e o cilindro e esboçar no plano, com as variações , , , esboçando
Resposta
Desenho feito conforme solicitado na questão.
Exercícios de Livros Relacionados
Escreva cinco outras integrais iteradas que sejam iguais à integral iterada dada. ∫ 0 1 ∫ 0 x 2 ∫ 0 y f x , y , zd z d y d x
Expresse a integral ∭ E f x , y , zd V como uma integral iterada de seis modos diferentes, onde E é o sólido limitado pelas superfícies dadas. x = 2 ,y = 2 ,z = 0 ,x + y - 2 z = 2
Expresse a integral ∭ E f x , y , zd V como uma integral iterada de seis modos diferentes, onde E é o sólido limitado pelas superfícies dadas. y = 4 - x 2 - 4 z 2 ,y = 0
Expresse a integral ∭ E f x , y , zd V como uma integral iterada de seis modos diferentes, onde E é o sólido limitado pelas superfícies dadas. y = x 2 ,z = 0 ,y + 2 z = 4
Escreva cinco outras integrais iteradas que sejam iguais à integral dada. ∫ 0 1 ∫ y 1 ∫ 0 z f x , y , zd xd zd y