Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 38
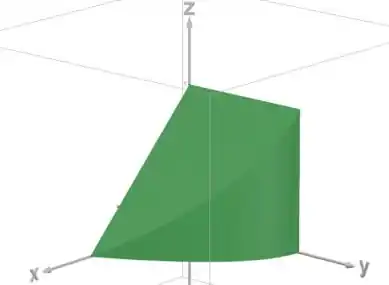
Esboce o sólido cujo volume é dado pela integral iterada.
Passo 1
E aii, galera!
Nessa questão a gente precisa esboçar um sólido, e o volume dele é dado por essa integral:
Pra isso, a gente vai lembrar que uma integral desse tipo:
Representa o volume do sólido entre o gráfico de e o plano , em um domínio .
Precisamos então descobrir quem é e , e ai conseguimos desenhar!
Passo 2
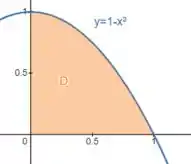
Vamos identificar primeiro o domínio no plano . Observe que varia entre e enquanto varia entre e . Assim, o domínio de integração é representado por
Passo 3
A função dentro da integral é:
Então a superfície que ela representa é:
Isso é um plano, que não depende de ! Pra desenhar ele a gente consegue desenhar a reta no plano e estender para o 3D:
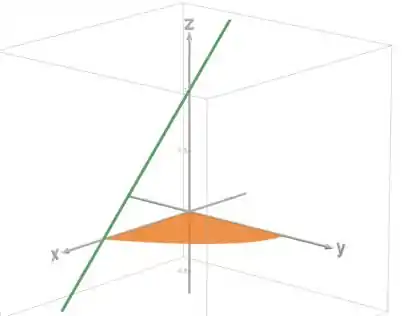
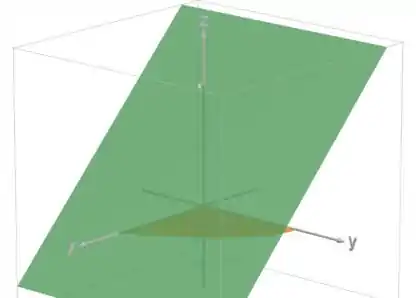
A região em laranja é o domínio
Como a integral é sobre , vamos pegar só a parte do plano sobre esse domínio:
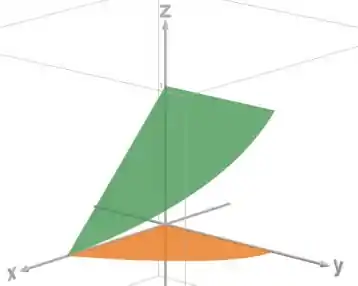
E nosso sólido vai ser a região entre essas duas superfícies:
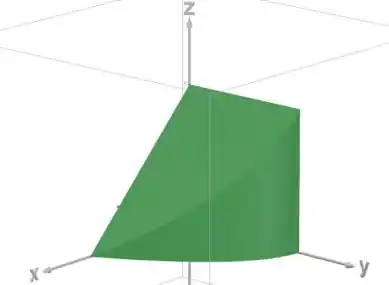
Resposta
