Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 36

Determine o volume do sólido por subtração de dois volumes.

O sólido delimitado pelo paraboloide cilíndrico y = x 2 e pelos planos z = 3 y e z = 2 + y .

Passo 1

Faala, pessoal!

Essa questão pede pra gente calcular um sólido usando subtração de dois volumes...

Como assim??

Lembra que o volume de um sólido embaixo do gráfico de uma função z = f x , y em um domínio D é calculado por essa integral:

∬ D f x , y d A

Então quando a gente tem um sólido que está entre o gráfico de duas funções f e g , o volume dele vai ser o volume embaixo de f menos o volume embaixo de g (ou vice-versa). Então, se f > g :

V = ∬ D f x , y d A - ∬ D g x , y d A = = ∬ D f x , y - g x , y d A

Ou, se g > f :

V = ∬ D g x , y d A - ∬ D f x , y d A = = ∬ D g x , y - f x , y d A

O que a gente vai fazer é identificar quem é f , g e D . Depois ver quem é maior que quem dentro desse domínio pra montar a integral que define o volume do sólido.

No final, vamos calcular essa integral.

Passo 2

Vamos ver as superfícies que limitam o sólido:

y = x 2

z = 3 y

z = 2 + y

As nossas funções vão ser:

f x , y = 3 y

g x , y = 2 + y

E a curva y = x 2 no plano x y vai limitar o domínio D :

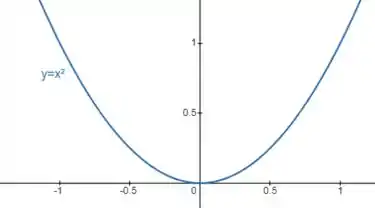
Só que ainda estamos com um domínio aberto... pra encontrar a outra limitação, vamos ver onde as funções f e g se interceptam:

3 y = 2 + y

2 y = 2 ⇒ y = 1

A reta y = 1 vai ser a outra limitação da região D :

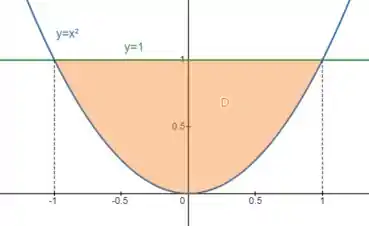
Agora a gente consegue expressar a região D com:

- 1 ≤ x ≤ 1

x 2 ≤ y ≤ 1

Passo 3

O próximo passo é descobrir qual das duas funções é maior que a outra nessa região. Pra isso, a gente pode testar qualquer ponto no interior de D , por exemplo 0 , 1 2 :

f 0 , 1 2 = 3 ∙ 1 2 = 3 2

g 0 , 1 2 = 2 + 1 2 = 5 2

Ou seja, em D , a função g é maior que f , e o volume do sólido vai ser:

V = ∬ D g x , y - f x , y d A

= ∬ D 2 + y - 3 y d A = ∬ D 2 - 2 y d A

Como sabemos que em D :

- 1 ≤ x ≤ 1

x 2 ≤ y ≤ 1

A integral fica assim:

V = ∫ - 1 1 ∫ x 2 1 2 - 2 y d y d x

Passo 4

Agora vamos calcular a integral, começando pela de y , mantendo x constante:

V = ∫ - 1 1 ∫ x 2 1 2 - 2 y d y d x =

= ∫ - 1 1 2 y - 2 y 2 2 x 2 1 d x =

Substituindo nos limites de integração:

= ∫ - 1 1 2 - 2 2 - 2 x 2 - 2 x 2 2 2 d x =

= ∫ - 1 1 1 - 2 x 2 + x 4 d x =

Podemos resolver a integral simples em função de x :

= x - 2 x 3 3 + x 5 5 - 1 1 =

= 1 - - 1 - 2 3 - - 2 3 + 1 5 - - 1 5 =

Resolvendo as contas:

= 2 - 4 3 - 2 5 = 30 - 20 + 6 15

⇒ V = 16 15

Resposta

V = 16 15  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume do sólido dado.Limitado pelo cilindro x 2 + y 2 = 1 e os planos y = z , x = 0 , z = 0 no primeiro octante.
Determine o volume do sólido dado.Limitado pelos cilindros z = x 2 , y = x 2 e os planos z = 0 , y = 4 .
Determine o volume do sólido por subtração de dois volumes.O sólido limitado pelos cilindros parabólicos y = 1 - x 2 , y = x 2 - 1 e pelos planos x + y + z = 2 , 2 x + 2 y - z + 10 = 0 .
Determine o volume do sólido dado.Limitado pelos planos z = x , y = x , x + y = 2 e z = 0
Determine o volume do sólido dado.Limitado pelo cilindro y 2 + z 2 = 4 e os planos x = 2 y , x = 0 , z = 0 no primeiro octante.