Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.9 - Ex. 13
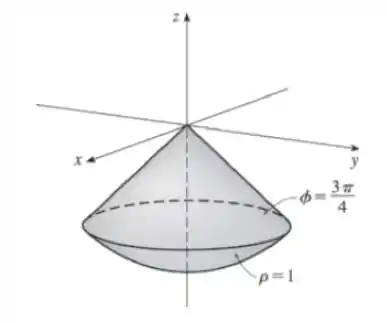
Esboce o sólido descrito pelas desigualdades dadas.
Passo 1
Olá, tudo bem? Sabemos das coordenadas esféricas que é uma esfera centrada na origem e de raio . Então o sólido é uma esfera sólida de raio .
Mas acabou? Não! Devemos dar uma olhada no ângulo .
Passo 2
Só é uma esfera completa se vai de até . Mas aqui o ângulo varia entre . Então é só a parte de baixo. É como se tivéssemos um sorvete com virado para baixo. Saca só como fica o desenho:
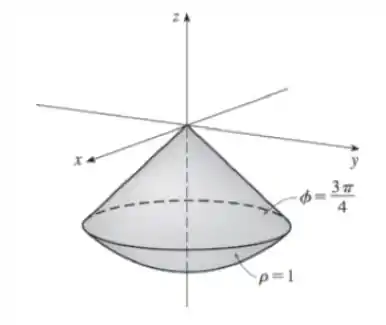
Por enquanto é isso pessoal, espero ter ajudado ;)
Beleza?
Vamos pra próxima?
Resposta
Exercícios de Livros Relacionados
Utilize as coordenadas esféricas.a) Determine o volume do sólido que está acima do cone ϕ = π / 3 e abaixo da esfera ρ = 4 cos ϕ .b) Encontre o centroide do sólido da parte (a).
Calcule a integral, transformando para coordenadas esféricas. ∫ - a a ∫ - a 2 - y 2 a 2 - y 2 ∫ - a 2 - x 2 - y 2 a 2 - x 2 - y 2 ( x 2 z + y 2 z + z 3 )d zd xd y
A latitude e a longitude de um ponto P no hemisfério norte estão relacionadas com as coordenadas esféricas ρ ,θ ,ϕ como a seguir. Tomamos a origem como o centro da Terra e o eixo z passando pelo norte
Determine o volume delimitado pelo toro ρ = s e n ϕ Utilize um computador para desenhar o toro