Esboce o sólido descrito pelas desigualdades dadas.
Passo 1
O problema pede para esboçarmos a região dada em coordenadas esféricas:
Assim, a região pedida está entre as esferas de raio e . Como vai de só até , apenas a parte com vaia aparecer, então estamos acima do plano . Por fim, como o ângulo polar vai de até , vamos pegar apenas o segundo e terceiro quadrantes!
Passo 2
O plot da região é dado a seguir:
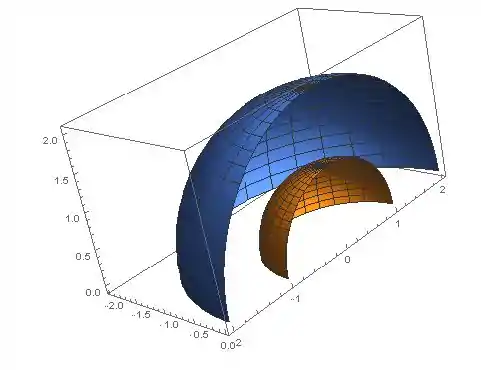
Resposta
Esboço de gráfico