Show de bola, galera! Partiu plotar o gráfico dessa região . Só não podemos nos esquecer de que nosso sitema de coordenadas cilíndricas tem a seguinte convenção:

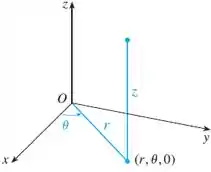
Vamos entender variável por variável:

• :

Como vemos na imagem acima, é um raio, uma distância da origem até o ponto que estamos considerando. O enunciado nos deu que:

Então o que temos aqui é a descrição de uma circunferência de raio 2 no plano .

Passo 3

• :

Como vemos na imagen, é nosso ângulo no plano partindo do eixo . Como o enunciado nos trouxe que:

Vemos que nosso sólido vai varia de partir do eixo no horário, por isso está negativo, até , partindo do eixo no sentido anti-horário, por isso ficou positivo. Somando o valor absoluto desses ângulos teremos:

E equivale a metade da circunferência.

Até agora sabemos que nosso sólido é um semicírculo de raio 2. Falta só entendermos a variação desse sólido no eixo .

Passo 4

• : o enunciado diz que:

Então nosso sólido parte do plano , onde e vai até o plano .

Então, finalemente podemos esboçar nosso sólido.

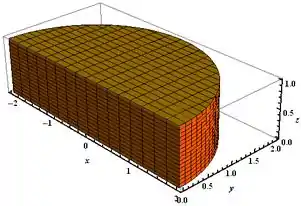
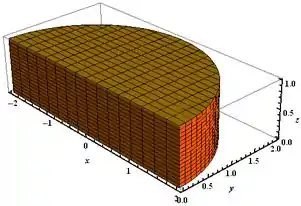
Semicírculo de raio 2 com altura de .