Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.9 - Ex. 19

Escreva a integral tripla de uma função contínua e arbitrária em coordenadas cilíndricas ou esféricas sobre o sólido mostrado

Passo 1

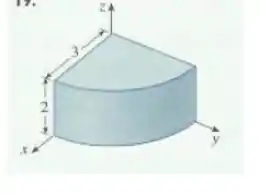
Oi galera, tudo bem? Aqui temos um pedaço de um cilindro, então a descrição mais adequada (fácil kkk) é utilizando as coordenadas cilíndricas. Sendo assim devemos determinar os limites de .

Como podemos ver da figura, tanto em quanto em o sólido vai de até . De forma circular. Então em coordenadas retangulares no plano temos:

A correspondência entre as coordenadas cilíndricas e cartesianas é:

E temos que em coordenadas cilíndricas: . Então temos:

Mas como queremos apenas a parte do primeiro quadrante:

Passo 2

Agora para . O ângulo contempla apenas o primeiro quadrante, então:

Passo 3

Legal! O próximo passo é determinar . A altura desse cilindro vai do plano , até o plano . Então a coordenada está entre:

Assim a integral de volume fica:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja D a calota menor cortada de uma esfera sólida de raio de2 unidades por um plano a uma distância de 1 unidade do centro da esfera. Expresse o volume de D como uma integral triplaiterada em coorden

Como são avaliadas integrais triplas em coordenadas cilíndricas e esféricas? Como são encontrados os limites de integra-ção? Dê exemplos.

Buraco em uma esfera Um buraco cilindrico é feito através de uma esfera sólida, o eixo do buraco sendo um diâmetro da esfera. O volume do restante do sólido é V = 2 ∫ 0 2 π ∫ 0 3 ∫ 1 4 - z 2 r d

Esfera e cilindro Encontre o volume do material cortado daesfera sólida r2 + z2 ≤ 9 pelo cilindro r = 3 sen u.

Coordenadas esféricas Encontre o volume da região delimitada pela superfície em coordenadas esféricas r = 2 sen f(veja a figura a seguir)