Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.5 - Ex. 84bc
b. Esboce
e
em um único gráfico para Como o comportamento de se compara com o de g?
Estime o valor de .
c. Confirme sua estimativa de com o cálculo pela regra de L’ Hopital.
Passo 1
b. Para esboçar esses gráficos, podemos por valores bem altos para x para avaliar o comportamento da função quando .
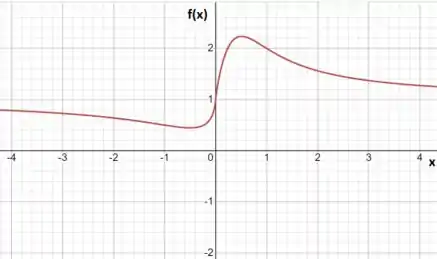
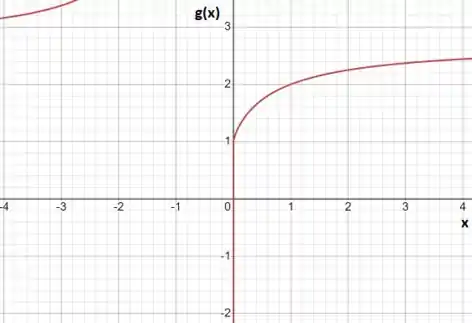
Passo 2
Analisando o gráfico podemos notar que a função vai para zero e a função tende a um valor .
Passo 3
c. Agora iremos resolver o limite por LH.
Passo 4
Primeiro iremos usar a regra
para reescrever o limite.
Passo 5
Temos então:
Usando as propriedades do limite:
Passo 6
Se a gente substituir o limite na função, temos uma indeterminação do tipo , então iremos ajeita essa função para que tenhamos 0/0 ou :
Passo 7
Podemos agora aplicar LH, derivando em cima e em baixo:
Passo 8
Como fugimos da indeterminação, agora podemos substituir o limite:
Pondo de volta na função original :