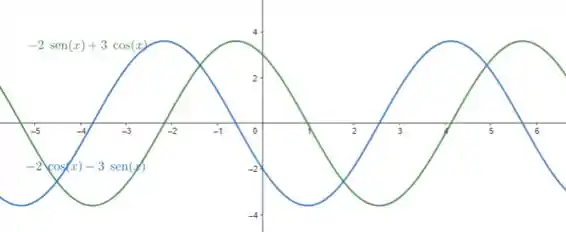
Uma tira elástica é presa a um gancho e uma massa é presa na ponta inferior da tira. Quando o corpo é puxado para baixo e então solto, ele vibra verticalmente. A equação do movimento é , onde é medido em centímetros e , em segundos. (Consideremos o sentido positivo como para baixo.)
- Encontre a velocidade e a aceleração no tempo .
- Faça os gráficos das funções velocidade e aceleração.
- Quando o corpo passa pela posição de equilíbrio pela primeira vez?
- A que distância da posição de equilíbrio o corpo chega?
- Quando a velocidade é máxima?
Passo 1
Fala, galera! Beleza? Seguinte... o enunciado nos dá a seguinte função que representa o movimento oscilatório de uma massa:
a) Encontre a velocidade e a aceleração no tempo
Esta parte do enunciado pede para determinar a velocidade e a aceleração do corpo vibrante em relação ao tempo. Para isso, primeiro calculamos a derivada da função posição em relação ao tempo para obter a velocidade , e então calculamos a derivada da velocidade em relação ao tempo para obter a aceleração
- Calcular a derivada de uma função trigonométrica composta, usando as regras de derivada para funções trigonométricas e funções compostas.
- Aplicar a regra da cadeia quando derivamos termos trigonométricos compostos.
b) Faça os gráficos das funções velocidade e aceleração:
Esta parte pede para representar graficamente as funções velocidade e aceleração em relação ao tempo . Podemos fazer isso usando software de plotagem, como MATLAB, Python com matplotlib, ou qualquer outra ferramenta de sua escolha.
- Plotar as funções velocidade e aceleração usando um gráfico de linha ou um gráfico de dispersão, dependendo da preferência ou requisitos do problema.
c) Quando o corpo passa pela posição de equilíbrio pela primeira vez:
Esta parte pede para determinar quando o corpo passa pela posição de equilíbrio pela primeira vez. Isso acontece quando a função posição é igual a zero.
- Resolver a equação para encontrar os valores de onde o corpo passa pela posição de equilíbrio.
- Selecionar o primeiro valor positivo de encontrado, pois estamos interessados na primeira passagem pela posição de equilíbrio.
d) A que distância da posição de equilíbrio o corpo chega:
Esta parte pede para determinar a distância da posição de equilíbrio que o corpo atinge. Isso é representado pela amplitude da oscilação, que é a distância máxima que o corpo se afasta do ponto de equilíbrio.
- Identificar os coeficientes dos termos seno e cosseno na função
- Usar esses coeficientes para calcular a amplitude da oscilação.
e) Quando a velocidade é máxima:
Esta parte pede para determinar quando a velocidade do corpo é máxima. Isso ocorre quando a derivada da velocidade em relação ao tempo é igual a zero.
- Resolver a equação para encontrar os valores de onde a velocidade é máxima.
- Usar o teste da segunda derivada para verificar se esses pontos são máximos ou mínimos. Se a segunda derivada for negativa, o ponto é um máximo.
Vamos lá! 😉
Passo 2
Derivando para encontrar , temos:
Para encontrar que é a derivada da função em relação ao tempo usamos a regra da soma e as regras de derivadas trigonométricas.
A regra da soma nos diz que a derivada da soma de duas funções é a soma das derivadas dessas funções individualmente. Vamos aplicar isso à função
Para encontrar a derivada de em relação a, derivamos cada termo em relação a
Agora, usamos as regras de derivadas trigonométricas:
Substituindo essas derivadas, temos:
Portanto, a velocidade em relação ao tempo é:
Passo 3
Derivando para encontrar a equação da aceleração , temos:
Para encontrar , que é a derivada da função em relação ao tempo , aplicamos novamente a regra da soma e as regras de derivadas trigonométricas.
A função foi encontrada anteriormente como a velocidade em função do tempo. Agora, vamos encontrar a aceleração derivando em relação a
Para encontrar a derivada de em relação a derivamos cada termo em relação a
Agora, usamos as regras de derivadas trigonométricas:
Substituindo essas derivadas, temos:
Portanto, a aceleração em relação ao tempo é:
Passo 4
Plotando o gráfico da velocidade em função do tempo, temos:
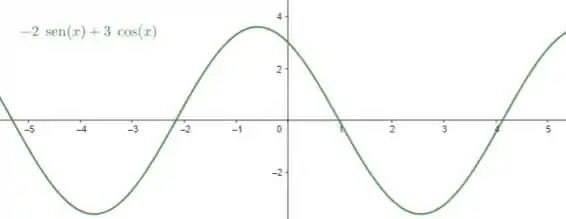
Plotando o gráfico da aceleração em função do tempo, temos:
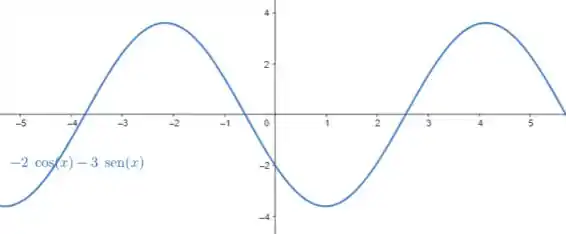
Passo 5
O corpo passa pela posição de equilíbrio pela primeira vez quando , portanto:
segundos
Passo 6
A maior distância da posição de equilíbrio que o corpo chega ocorre quando .
Assim, vamos primeiro descobrir o tempo em que isso ocorre:
segundos
Assim, substituindo esse valor na equação da posição, iremos encontrar:
cm
Passo 7
A velocidade será máxima () quando o corpo passar pela posição inicial, logo:
Logo, como vimos no Passo 5, o corpo irá passar pela posição inicial em:
Onde é um inteiro positivo.
Entendeu direitinho?? Responde aee 😉
Resposta
- e ;