Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 70

Uma escada deverá passar por cima de um muro de 27 8   m de altura e alcançar uma parede que está a 8   m depois do muro. Ache o menor comprimento que a escada a ser usada pode ter.

Passo 1

A primeira coisa a se fazer nessa questão é um esboço do que está acontecendo. Segue o esboço com a escada, muro e parede.

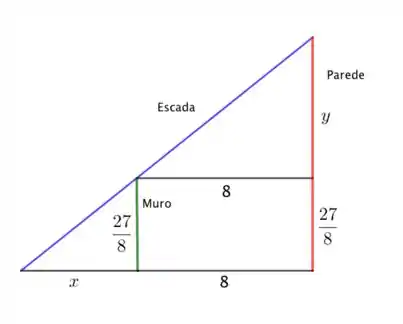
Perceba que adicionei os comprimentos x e y . O comprimento C da escada é justamente a hipotenusa de um triângulo retângulo. Podemos escrever o seguinte:

C 2 = x + 8 2 + y + 27 8 2   →       C = x + 8 2 + y + 27 8 2                 x , y > 0

Agora vamos tentar deixar o x em função de y usando semelhança de triângulos. Basta perceber que:

x 8 = 27 8 y   →       x = 27 y

Substituindo em C temos:

C ( y ) = 27 y + 8 2 + y + 27 8 2

Passo 2

Para achar o menor comprimento, vamos derivar essa função que depende apenas dos valores de y e igualar 0 .

C ' y = 27 y - 1 + 8 2 + y + 27 8 2 ' 2 27 y + 8 2 + y + 27 8 2 = 27 y - 1 + 8 27 y - 1 ' + y + 27 8 27 y + 8 2 + y + 27 8 2

C ' y = - 27 y + 8 27 y 2 + y + 27 8 27 y + 8 2 + y + 27 8 2 = - 27 2 y 3 - 8 ⋅ 27 y y 3 + y + 27 8 27 y + 8 2 + y + 27 8 2

C ' y = y - 8 ⋅ 27 y y 3 + 27 8 - 27 2 y 3 27 y + 8 2 + y + 27 8 2 = y 1 - 8 ⋅ 27 y 3 + 27 8 1 - 8 ⋅ 27 y 3   27 y + 8 2 + y + 27 8 2

C ' y = 1 - 8 ⋅ 27 y 3 y + 27 8 27 y + 8 2 + y + 27 8 2 = 0     →           1 - 8 ⋅ 27 y 3 y + 27 8 = 0

Daí, y + 27 8 = 0 não pode, pois y > 0 e temos 1 - 8 ⋅ 27 y 3 = 0   →     y 3 = 8 ⋅ 27 →       y = 2 ⋅ 3 = 6 . Sendo assim, o ponto crítico é y = 6 .

Perceba agora que se y > 6 , então C ' y > 0 e se y < 6 , então C ' y < 0 . Isso indica que nós temos o ponto de mínimo absoluto no y = 6 .

O menor comprimento será C 6 = 75 6 2 + 75 8 2 = 75 2 ⋅ 3 2 + 75 2 ⋅ 4 2 = 75 2 3 2 2 + 75 2 4 2 2

= 16 75 2 2 + 9 75 2 2 144 = 5 2 75 2 2 12 2 = 5 ⋅ 75 2 ⋅ 12 = 375 24 = 125 8   m

Resposta

O menor comprimento é 125 8   m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre as dimensões de um retângulo com área de 1000m 2 cujo perímetro seja o menor possível.
Um container para estocagem retangular com uma tampa aberta deve ter um volume de 10m 3 . O Comprimento da base é o dobro da largura. O material para a base custa $ 10 por metro quadrado. O material p
Uma caixa com uma base quadrada e sem tampa tem volume de 32000c m 3 . Encontre as dimensões da caixa que minimizam a quantidade de material usado.
Considere o seguinte problema: um fazendeiro com 300 m de cerca quer cercar uma área retangular e então dividi-la em quatro partes com cercas paralelas a um lado do retângulo. Qual é a maior área tota
Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. (O diâmetro do semicírculo é igual à largura do retângulo). Se o perímetro da janela for 30p é s é , encontre as dimensões