Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.15 - Ex. 18
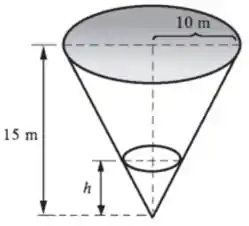
Enche-se um reservatório, cuja forma é a de um cone circular reto, de água a uma taxa de m³/s. O vértice está a m do topo e o raio do topo é de m. Com que velocidade o nível da água está subindo no instante em que m.
Passo 1
Primeiramente devamos relacionar o volume de água com a altura :
Se o volume do cone é dado por:
Onde é o raio na altura .
Temos que para toda altura temos um raio que é proporcional a ele, ou seja:
Assim, o volume é dado por:
Passo 2
Derivando em função do tempo, temos:
Assim, se o volume de água cresce a uma taxa de m³/s, ou seja, e , temos:
Logo, a velocidade com que o nível da água está́ subindo é m/s.
Resposta
A velocidade com que o nível da água está́ subindo é m/s.
Exercícios de Livros Relacionados
Seja f t = t t 2 + 4 .a) Estude o sinal de f ' t .b) Estude o sinal de f ' ' t .c) Calcule lim t → + ∞ t t 2 + 4 e lim t → - ∞ t t 2 + 4 .d) Utilizando as informações acima, esboce o gráfico de f
Uma partícula desloca-se sobre o eixo x com função de sua posição x = 3 + 2 t - t 2 , t ≥ 0 .a) Qual a velocidade no instante t ?b) Qual a aceleração no instante t ?c) Estude a variação do sinal de v
A equação do movimento de uma partícula que se desloca ao longo do eixo x é x = e - t sen t , t ≥ 0 .a) Determine a velocidade e a aceleração no instante t .b) Calcule lim t → + ∞ e - t sen t .c
A posição de uma partícula que se desloca ao longo de eixo x varia com o tempo segundo a equação x = v 0 k 1 - e - k t , t ≥ 0 , em que v 0 e k são constantes estritamente positivas.a) Qual a velocida
Suponha que os comprimentos dos segmentos A B e 0 B sejam, respectivamente, 5c m e 3c m . Suponha, ainda, que θ esteja variando a uma taxa constante de 1 2 rad/s. Determine a velocidade de A , quando