Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.15 - Ex. 3

A posição de uma partícula que se desloca ao longo de eixo x depende do tempo de acordo com a equação x = - t 3 + 3 t 2 , t ≥ 0 .

a) Estude o sinal de v t .

b) Estude o sinal de a t .

c) Calcule lim t → ∞ ⁡ - t 3 + 3 t 2 .

d) Esboce o gráfico da função x = - t 3 + 3 t 2 , t ≥ 0 .

Passo 1

a) A velocidade, é a taxa com que a posição muda no tempo, ou seja, a derivada em t .

Assim:

v t = x ' t = - 3 t 2 + 6 t

Temos então, que a velocidade descreve uma parábola com a concavidade voltada para baixo, assim, a parte positiva está entre suas raízes e a negativa está na região externa a suas raízes.

Como as raízes são:

- 3 t 2 + 6 t = 0

3 t - t + 2 = 0

t = 0

Ou

t = 2

Assim, temos que v t > 0 se 0 < t < 2 e v t < 0 se t > 2 .

Passo 2

b) De modo análogo, a aceleração é a taxa com que a velocidade muda no tempo, ou seja, a derivada em t .

a t = v ' t = - 6 t + 6

a t = - 6 t + 6

Como a aceleração descreve uma reta decrescente, então, antes da raiz ela assume apenas valores positivos, e após a raiz, ela assume valores negativos.

Temos que a raiz é

- 6 t + 6 = 0

6 t = 6

t = 1

então:

v t > 0 se 0 ≤ t < 1 e v t < 0 se t > 1 .

Passo 3

c) Para calcular o limite, devemos colocar o t 3 em evidência:

- t 3 + 3 t 2 = t 3 - 1 + 3 t

Logo:

lim t → ∞ ⁡ - t 3 + 3 t 2 = lim t → ∞ ⁡ t 3 - 1 + 3 t = + ∞ ⋅ - 1 + 0

lim t → ∞ ⁡ - t 3 + 3 t 2 = - ∞

Passo 4

d) O gráfico de x = - t 3 + 3 t 2 para t ≥ 0 é dado por:

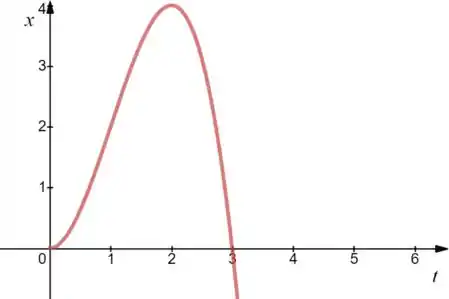
Resposta

a) v t > 0 se 0 < t < 2 e v t < 0 se t > 2 .

b)   v t > 0 se 0 ≤ t < 1 e v t < 0 se t > 1 .

c)

lim t → ∞ ⁡ - t 3 + 3 t 2 = - ∞

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja x = f t , t ≥ 0 , tal que f 0 = 1 , d x d t0 e d 2 x d t 20 para t ≥ 0 . Como você acha que deve ser o gráfico de f ? Por quê?
Uma partícula desloca-se sobre o eixo x com função de posição x = 1 2 t + 1 , t ≥ 0 .a) Qual a velocidade no instante t ?b) Qual a aceleração no instante t ?c) Esboce o gráfico da função de posição.
Um ponto P move-se sobre a parábola y 2 = x , x0 e y0 . A abscissa x está variando com uma aceleração que, em cada instante, é o dobro do quadrado da velocidade da ordenada y . Mostre que a ordena
O ponto P = x ,y está fixo à roda de raio 1 m, que rola, sem escorregamento, sobre o eixo x . O ângulo θ está variando a uma taxa constante de 1 rad/s. Expresse as velocidades da abscissa e da orde
Um ponto P move-se ao longo do gráfico de y = 1 x 2 + 1 de tal modo que a sua abscissa x varia a uma velocidade constante de 5 (m/s). Qual a velocidade de y no instante em que x = 10m ?