Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.4 - Ex. 33
Uma escada com pés de comprimento está apoiada em uma parede vertical. Seja o ângulo entre o topo da escada e a parede, e a distância da base da escada ate a parede. Se a base da escada escorregar para longe da parede, com que rapidez variará em relação a quando ?
Passo 1
Opa, bora lá! Temos uma escada com pés de comprimento apoiada em uma parede fazendo um ângulo com a parede da seguinte forma:
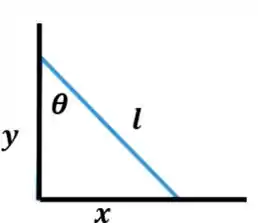
Supondo que a escada escorregue queremos saber quem é quando !
Como ele nos pede para relacionar o ângulo com o , podemos usar a o , olha só:
Logo,
Passo 2
Como queremos achar a rapidez de em relação a , basta acharmos . Assim, vamos derivar a relação que achamos no Passo 1.
Derivando:
Passo 3
Como queremos saber para o momento em que :
Como pés e :
Portanto,
Prontinho!