Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.5 - Ex. 59

Determine as equações paramétricas da reta intersecção dos planos.

5 x - 2 y - 2 z = 1

Passo 1

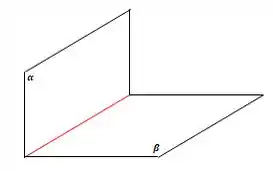
A reta que queremos descobrir é a reta em vermelho que é a interseção entre os dois planos.

Primeiro iremos encontrar um ponto da reta. Podemos escolher qualquer ponto dela, vamos escolhar o ponto onde a reta intercepta o plano x y colocando z = 0 . Com isso teremos as seguintes equação para os planos dados:

5 x - 2 y = 1   I 4 x + y = 6   I I

I I × 2 + I → 13 x = 13

x = 1

Substituindo esse valor de x nas equações acima chegamos que y = 2 .

Passo 2

Agora vamos encontrar o vetor normal de cada plano dado

5 x - 2 y - 2 z = 1 → n 1 = 5 , - 2 , - 2 4 x + y + z = 6 → n 2 = 4,1 , 1

Como esses vetores normais são perpendiculares aos planos acima temos que a reta, que pertence a ambos os planos, é ortogonal aos vetores normais, com isso temos que o produto vetorial entre os vetores normais resulta em um vetor paralelo à essa reta.

v = n 1 × n 2 = i j k 5 - 2 - 2 4 1 1 =

= i ∙ - 2 ∙ 1 + j ∙ - 2 ∙ 4 + k ∙ 5 ∙ 1 - i ∙ 1 ∙ - 2 + j ∙ 5 ∙ 1 + k ∙ - 2 ∙ 4 =

= - 2 i - 8 j + 5 k + 2 i - 5 j + 8 k =

= - 13 j + 13 k

Passo 3

Com o ponto de intersecção as coordenadas do vetor encontrado achamos o quê queríamos.

Equação paramétrica: y - 2 - 13 = z 13

Resposta

Equação paramétrica: y - 2 - 13 = z 13

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se os planos são paralelos, perpendiculares, ou nenhum. Se não, ind ind o ângulo entre eles. (Arredondar uma casa decimal.) 5 x + 2 y + 3 z = 2 y = 4 x - 6 z
Encontre uma equação de plano para um plano que passe pelo ponto ( 1,5 , 1 ) perpendicular aos planos 2 x + y - 2 z = 2 e x + 3 z = 4 .
Determine se os planos são paralelos, perpendiculares, ou nenhum. Se não, ind ind o ângulo entre eles. (Arredondar uma casa decimal.) 9 x - 3 y + 6 z = 2 2 y = 6 x + 4 z
Onde a linha que passa por (- 3,1 , 0) e (- 1,5 , 6) intercepta o plano 2 x + y - z = - 2
Determine se os planos são paralelos, perpendiculares, ou nenhum. Se não, ind ind o ângulo entre eles. (Arredondar uma casa decimal.) 2 x - 3 y = z 4 x = 3 + 6 y + 2 z