Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 23

  1. Expresse o volume da cunha no primeiro octante que é cortada do cilindro y 2 + z 2 = 1 pelos planos y = x e x = 1 como uma integral tripla.
  2. Utilize a Tabela de Integrais (nas Páginas de referência 6-10) ou sistema de computação algébrica para determinar o valor exato da integral tripla da parte (a).

Passo 1

Fala, turma! Tudo certo?

A questão tem duas partes. A parte a) pede para expressarmos o volume da cunha que está no primeiro octante e que é cortada pelo cilindro

y 2 + z 2 = 1

E pelos planos:

y = x e x = 1

Como uma integral tripla.

O volume de um sólido como uma integral tripla é dado por:

V = ∭ E 1   d V

E:

d V = d x   d y   d z

Onde os limites de integração de E a gente vai tirar da descrição da região no enunciado.

A parte b) pede para usarmos a tabela de integrar ou um sistema de computação algébrica para acharmos o valor exato da integral tripla.

Vamos lá!

Passo 2

  1. Para calcular o volume, vamos calcular a integral

    2. V = ∭ E 1   d V

    Vamos começar achando os limites de integração.

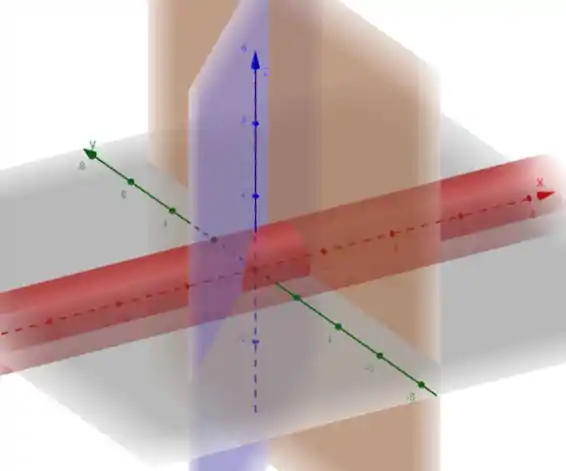
    Temos que, no primeiro octante, a variação de z é de 0 até o cilindro. Isolando z na equação, temos:

    y 2 + z 2 = 1

    z 2 = 1 - y 2

    Aplicando a raiz quadrada dos dois lados da equação:

    z = ± 1 - y 2

    No primeiro octante pegamos a parte positiva só, então temos

    0 ≤ z ≤ 1 - y 2

    O y vai variar entre o plano

    y = 0 e y = x

    Então

    0 ≤ y ≤ x

    Agora falta achamos os limites de x . Como temos somente o primeiro octante, sabemos que o menor valor de x é zero. Como nosso sólido está limitada no plano x = 1 , nossos limites de integração são:

    0 ≤ x ≤ 1

    A integral fica então

    V = ∭ E 1   d V = ∫ 0 1 ∫ 0 x ∫ 0 1 - y 2 d z d y d x

    Aqui a gente coloca as integrais com variáveis nos limites de integração “pra dentro” da integral.

    Passo 3

  2. Calculando a integral, começando pela integral de dentro em relação a z :

∫ 0 1 ∫ 0 x ∫ 0 1 - y 2 d z d y d x = ∫ 0 1 ∫ 0 x z 0 1 - y 2 d y d x

Aplicando os limites de integração:

∫ 0 1 ∫ 0 x 1 - y 2   d y d x

Focando agora só na integral de dentro em função de y :

∫ 1 - y 2   d y

Vamos fazer uma substituição para facilitar nossos cálculos. Substituindo

y = sen ⁡ θ

Derivando y :

d y = cos ⁡ θ d θ

Substituindo:

∫ 1 - y 2   d y = ∫ 1 - sen 2 ⁡ θ   cos ⁡ θ d θ

Usando a identidade:

1 - sen 2 ⁡ θ = cos 2 ⁡ θ

Substituindo:

= ∫ cos 2 ⁡ θ cos ⁡ θ d θ = ∫ cos 2 ⁡ θ d θ

Reescrevendo:

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

Podemos finalmente calcular a integral:

= ∫ 1 + cos ⁡ 2 θ 2 d θ = θ 2 + sen ⁡ 2 θ 4 + C

= θ 2 + sen ⁡ θ cos ⁡ θ 2 + C

Passo 3

Para voltarmos para a variável y , vamos usar o triangulo:

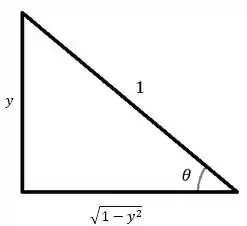
Então temos que, pela substituição

sen ⁡ θ = y

e pelo triangulo

cos ⁡ θ = 1 - y  

logo

∫ 1 - y 2   d y = arcsen ⁡ y 2 + y 1 - y 2 2 + C

Então temos que:

∫ 0 1 ∫ 0 x 1 - y 2   d y d x =

Aplicando os limites de integração:

= ∫ 0 1 arcsen ⁡ x 2 + x 1 - x 2 2 d x

Usando agora a página de referência

∫ arcsen ⁡ x d x = x arcsen ⁡ x + 1 - x 2 + C

E a outra integral conseguimos fazer por substituição

∫ x 1 - x 2   d x

Substituindo

u = 1 - x 2

Derivando u , temos:

d u = - 2 x   d x

Substituindo:

∫ x 1 - x 2   d x = - 1 2 ∫ u   d u

Calculando a integral:

= - 1 2 2 u 3 2 3 = - u 3 2 3 + C

Substituindo o valor de u :

= - 1 - x 2 3 2 3 + C

Então temos

∫ 0 1 arcsen ⁡ x 2 + x 1 - x 2 2 d x = 1 2 x arcsen ⁡ x + 1 - x 2 - 1 - x 2 3 2 3 0 1

Aplicando os limites de integração:

= 1 2 arcsen ⁡ 1 - 1 - 1 3 2 3

Temos que arcsen ⁡ 1 = π / 2

= 1 2 π 2 - 1 - 1 3 = 1 2 π 2 - 2 3

Simplificando:

= π 4 - 1 3

Resposta

  1. V = ∫ 0 1 ∫ 0 x ∫ 0 1 - y 2 d z d y d x

= π 4 - 1 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular o volume do sólido acima do plano xy e interior às superfícies z = 9 - x 2 - y 2 e x 2 + y 2 = 1 .
Calcular o volume do tetraedro delimitado pelos planos coordenados e pelo plano x a + y b + z c = 1 .
Nos exercícios 11 a 19, calcular o volume do sólido delimitado pelas superfícies dadas.11. x 2 + y 2 = 16 ; z = 2 e x + z = 9 .
Calcular o volume do sólido delimitado por z = 8 - x 2 - 2 y 2 , no primeiro octante.
Calcular o volume da parte da esfera x 2 + y 2 + z 2 = 9 entre os planos z = 1 e z = 2 .