Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 13.4 - Ex. 4
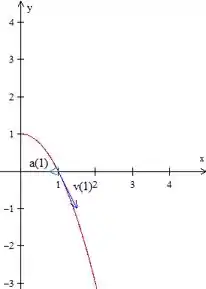
Determine a velocidade, a aceleração e a velocidade escalar da partícula cuja função posição é dada. Esboce a trajetória da partícula e desenhe os vetores velocidade e aceleração para os valores de especificados.
Passo 1
Olá, meu esforçado e inteligente aluno. Vamos resolver juntos mais uma atividade hoje.
Dada a equação da posição:
Uma partícula que tem uma função vetorial de posição do tipo:
Vamos encontrar as equações da velocidade, aceleração e a velocidade escalar dessa partícula.
Tem como função vetorial velocidade:
Velocidade escalar:
E vetor aceleração:
Passo 2
Queremos calcular o vetor velocidade, velocidade escalar e aceleração, e após isso, esboçar a curva da seguinte função vetorial, desenhando o vetor aceleração e posição no ponto:
O vetor posição em é:
Vamos calcular a velocidade:
E para esse caso, temos que:
Então substituindo na relação para velocidade:
Em :
Passo 3
A velocidade escalar da partícula em é:
E para esse caso, temos que:
E a derivada é:
Então o modulo será:
Passo 4
O vetor aceleração da partícula é:
Ou podemos escrever como a derivada segunda da equação da posição:
Temos que:
Passo 5
Para esboçar a curva, vamos transformar a equação paramétrica em equação cartesiana:
Aplicando em :
Que é uma parábola, mas somente para . Seu gráfico é:
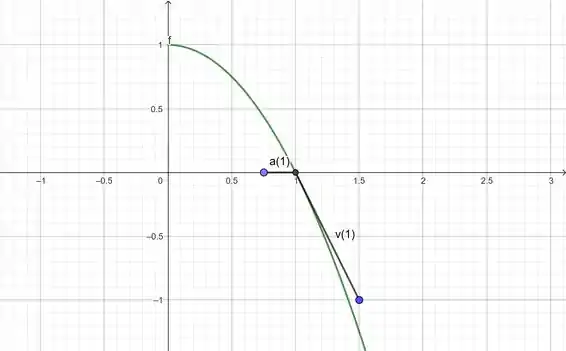
Então temos aqui o nosso gráfico, onde o vetor possui unidades para esquerda e está apenas na horizontal. Já o vetor velocidade possui unidade para a direita, e unidade para baixo.
Resposta
