Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 20

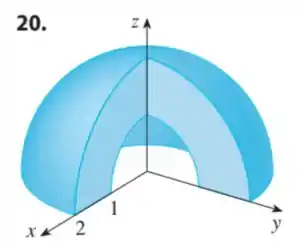
Escreva a integral tripla de uma função contínua arbitrária f x , y , z em coordenadas cilíndricas ou esféricas sobre o sólido mostrado.

Passo 1

Fala, pessoal!

Essa questão é moleza, relaxa aí!

Ela quer uma integral tripla de uma função f x , y , z que represente essa região em azul da imagem, tranquilo?

Daí precisamos ver se faremos pelas coordenadas cilíndricas ou esféricas.

Pela imagem, sabemos que é uma esfera oca, né verdade?

Então iremos utilizar as coordenadas esféricas!

Relembrando, temos:

x = ρ s e n ϕ cos ⁡ θ y = ρ sen ⁡ ϕ sen ⁡ θ , z = ρ cos ⁡ ϕ ρ 2 = x 2 + y 2 + z 2 d V = ρ 2 sen ⁡ ϕ d ρ d θ d ϕ

Belê! 😊

Passo 2

Como esse problema fica melhor escrito em coordenadas esféricas, vamos substituir o que temos:

∭ E f x , y , z d V =

∫ c d ∫ α β ∫ a b f ρ sen ⁡ ϕ cos ⁡ θ , ρ sen ⁡ ϕ sen ⁡ θ , ρ cos ⁡ ϕ ρ 2 sen ⁡ ϕ d ρ d θ d ϕ

Onde E é uma cunha esférica dada por:

E = ρ , θ , ϕ | a ≤ ρ ≤ b , α ≤ θ ≤ β , c ≤ ϕ ≤ d

Onde ρ é a distância da origem ao ponto, θ é o ângulo formado em relação ao eixo x e ϕ é o ângulo formado em relação ao eixo z.

Passo 3

Temos então pela figura que:

1 ≤ ρ ≤ 2

π 2 ≤ θ ≤ 2 π

0 ≤ ϕ ≤ π 2

Pronto, agora é só substituir:

∫ 0 π 2 ∫ π 2 2 π ∫ 1 2 f ρ sen ⁡ ϕ cos ⁡ θ , ρ sen ⁡ ϕ sen ⁡ θ , ρ cos ⁡ ϕ ρ 2 sen ⁡ ϕ d ρ d θ d ϕ

Molezaaa!😉

Resposta

∫ 0 π 2 ∫ π 2 2 π ∫ 1 2 f ρ sen ⁡ ϕ cos ⁡ θ , ρ sen ⁡ ϕ sen ⁡ θ , ρ cos ⁡ ϕ ρ 2 sen ⁡ ϕ d ρ d θ d ϕ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do conjuntox^2 + y^2 + z^2 = 2 * a * x e z = sqrt(x^2 + y^2) , a0 .
Calculee) int int int_B z * d x * d y * d z onde B é conjuntoz = sqrt(x^2 + y^2) , x^2 + y^2 + z^2 = 1 .
Calculec) int int int_B x * d x * d y * d z onde B é o conjunto (x^2)/(4) + (y^2)/(9) + z^2 = 1 , x = 0 .
Calculeb) int int int_B z * d x * d y * d z onde B é o conjunto z = 0 , 1 = x^2 + y^2 + z^2 = 4 .
Calcule a massa do sólido x 2 + y 2 + z 2 ≤ 1 e z ≥ x 2 + y 2 Supondo que a densida no ponto ( x , y , z ) é proporcional à distância deste ponto ao plano x y .