Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.9 - Ex. 20

Utilize a transformação dada para calcular a integral.

∬ R y 2 d A , onde R é a região limitada pelas curvas x y = 1 , x y = 2 , x y 2 = 1 , x y 2 = 2 ; u = x y , v = x y 2 .

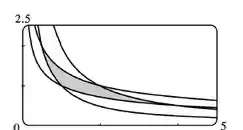
Ilustre utilizando uma calculadora gráfica ou um computador para traçar R .

Passo 1

Para calcular essa integral vamos usar:

∬ R f x , y d A = ∬ S f x u , v , y u , v ∂ x , y ∂ u , v d A

Primeiro vamos achar o jacobiano, que é da seguinte forma:

∂ x , y ∂ u , v = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

Temos:

u = x y → y = u x

v = x y 2 → v = x u x 2 = x u 2 x 2 = u 2 x → x = u 2 v

u = x y → y = u x = u u 2 v = u . v u 2 = v u

Vamos então calcular cada elemento e fazer a substituição.

Passo 2

Temos que ∂ x ∂ u é a derivada de x em função de u :

∂ x ∂ u = ∂ ∂ u u 2 v = 2 u v

E ∂ x ∂ v é a derivada de x em função de v :

∂ x ∂ v = ∂ ∂ v u 2 v = - u 2 v 2

Temos que ∂ y ∂ u é a derivada de y em função de u :

∂ y ∂ u = ∂ ∂ u v u = - v u 2

E por ultimo ∂ y ∂ v é a derivada de y em função de v :

∂ y ∂ v = ∂ ∂ v v u = 1 u

Passo 3

Pronto, agora é só substituir e calcular:

∂ x , y ∂ u , v = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v = 2 u v - u 2 v 2 - v u 2 1 u = 2 u v . 1 u - - u 2 v 2 - v u 2 = 2 v - 1 v = 1 v

Passo 4

Podemos ver a região R como:

1 < x y < 2

1 < x y 2 < 2

E como temos que u = x y e v = x y 2 :

1 < x y < 2 → 1 < u < 2

1 < x y 2 < 2 → 1 < v < 2

Agora temos 1 < v < 2 e 1 < u < 2 , no plano u v .

Passo 5

Agora vamo substituir na integral:

∬ R y 2 d A = ∬ S f x u , v , y u , v ∂ x , y ∂ u , v d A = ∫ 1 2 ∫ 1 2 v u 2 1 v   d v d u = ∫ 1 2 ∫ 1 2 v u 2   d v d u = ∫ 1 2 v d u ∫ 1 2 1 u 2 d u = v 2 2 1 2 - 1 u 1 2 = 2 2 2 - 1 2 2 - 1 2 - - 1 1 = 3 4

Resposta

∬ R y 2 d A = 3 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a imagem do conjunto S sob a transformação dada. S é o disco dado por u 2 + v 2 ≤ 1 ; x = a u , y = b v
Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Determine a imagem do conjunto S sob a transformação dada. S é o quadrado limitado pelas retas u = 0 , u = 1 , v = 0 , v = 1 ; x = v , y = u 1 + v 2
Utilize a transformação dada para calcular a integral. ∬ R x 2 d A , onde R é a região limitada pela elipse 9 x 2 + 4 y 2 = 36 ; x = 2 u , y = 3 v