Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.2 - Ex. 57
Escreva, mas não calcule, uma integral que represente a área da superfície obtida pela rotação da curva dada ao redor do eixo x.
Passo 1
Olá, meu querido e esforçado amigo. Vou te ajudar a resolver essa atividade, sei que parece superdifícil, mas irei fazer você sentir que ela é como roubar doce de criança.
Dada a curva parametrizada:
Queremos encontrar a área da superfície gerada quando rotacionamos a nossa curva parametrizada em torno do eixo .
Podemos visualizar abaixo a situação da superfície sendo rotacionada entorno de .
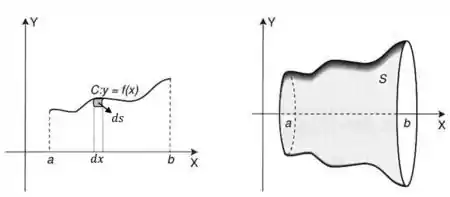
A área de uma superfície parametrizada rotacionada entorno de é dada por:
Sendo que
Precisamos então calcular as derivadas das parametrizações e precisamos depois disso montar a integral.
Passo 2
Então vamos calcular primeiro :
Aqui a gente vai precisar utilizar a regra do produto para derivar:
Agora para :
Então vamos ter:
Montando nossa integral:
E é isso meu amigo, temos aqui a nossa integral.