Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.1 - Ex. 6

  1. Mostre que cada membro da família de funções y = C e x 2 2 é uma solução da equação diferencial y ' = x y .
  2. Ilustre a parte (a) traçando vários membros da família de soluções na mesma tela.
  3. Encontre a solução da equação diferencial y ' = x y   que satisfaça a condição inicial y 0 = 5 .
  4. Encontre a solução da equação diferencial y ' = x y que satisfaça a condição inicial y 1 = 2 .

Passo 1

  1. Queremos mostrar que y = C e x 2 2 é solução de y ' = x y . Então vamos derivar a função de y e substituir na EDO.

    2. y = C e x 2 2

    y ' = x C e x 2 2

    Substituindo...

    y ' = x y

    x C e x 2 2 = x C e x 2 2  

    Passo 2

    3. Passo 3

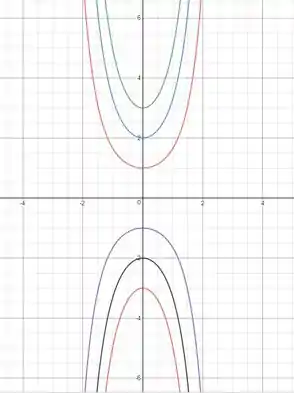
  3. Queremos encontrar uma solução de y ' = x y   tal que y 0 = 5

    4. Vimos no item (a) que y = C e x 2 2 é uma solução, portanto basta olharmos para a condição inicial.

    y 0 = C e 0 2 2 = 5

    C = 5

    Então encontramos y = 5 e x 2 2 como solução do problema de valor inicial.

    Passo 4

  4. Precisamos encontrar uma solução de y ' = x y tal que y 1 = 2

Sabemos do item (a) que y = C e x 2 2 é uma solução, então vamos analisar a condição inicial.

y 1 = C e 1 / 2 = 2

C = 2 e 1 / 2

Portanto, uma solução encontrada é y = 2 e 1 / 2   e x 2 2

Resposta

(c) y = 5 e x 2 2

(d) y = 2 e 1 / 2   e x 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra um circuito contendo uma força eletromotriz, um capacitor com capacitância de C Farads (F) e um resistor com resistência de R ohms (Ω). A queda de voltagem no capacitor é Q / C onde Q
No Exercício 14 na Seção 9.1 consideramos uma xícara de café a 95 ° C em uma sala com temperatura de 20 ° C . Suponha que o café esfrie a uma taxa de 1 ° C por minuto quando sua temperatura for 70 ° C
Use o método de Euler com cada um dos passos dados para estimar o valor de y 0,4 onde y é a solução do problema de valor inicial y ' = y ,y 0 = 1 .h=0,4h=0,2h=0,1Sabemos que a solução exata do problem
É mostrado um campo de direções para a equação diferencial y ' = y 1 - 1 4 y 2 . Esboce os gráficos das soluções que satisfazem as condições iniciais dadas. y 0 = 1 y 0 = - 1 y 0 = - 3 y 0 = 3 Ache to
É mostrado um campo de direções para a equação diferencial y ' = x s e n y .Esboce os gráficos das soluções que satisfazem as condições iniciais dadas. y 0 = 1 y 0 = 2 y 0 = π y 0 = 4 y 0 = 5 Ache tod