Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 1.4 - Ex. 12

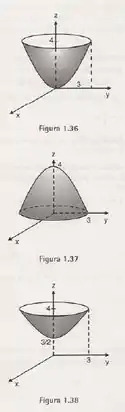
Escrever a função que representa o parabolóide circular das figuras 1.36, 1.37 e 1.38.

Passo 1

Para a figura 1.36, temos um parabolóide com concavidade para cima e vértice na origem.

Podemos ver que o ponto z ( 0,3 ) = 4 , usando a equação z = c ( x 2 + y 2 ) , obtemos

4 = c 0 2 + 3 2

4 9 = c

Logo, a equação para esse paraboloide é: z = 4 9 ( x 2 + y 2 ) .

Passo 2

Para a figura 1.37, temos o vértice do parabolóide no ponto ( 0 , 0,4 ) e o mesmo tem a concavidade para baixo. Usamos então, a equação z = 4 - c ( x 2 + y 2 ) e obtemos

4 = 4 - c ( 0 2 + 0 2 )

c = 4 9

Logo, a equação para esse paraboloide é: z = 4 - 4 9 ( x 2 + y 2 ) .

Passo 3

Para a figura 1.38 temos o vértice no ponto ( 0 , 0 , 3 2 ) , enquanto o paraboloide está virado para cima e tem curva de nível para z = 4 igual a x 2 + y 2 = 9 .

Usando as equações z = 3 2 + c ( x 2 + y 2 ) e z ( 0,3 ) = 4 , obtém-se

4 = 3 2 + c ( 9 )

5 2 = c ( 9 )

c = 5 18

Logo, a equação é z = 3 2 + 5 18 ( x 2 + y 2 ) .

Prontinho!

Resposta

z = 4 - 4 9 ( x 2 + y 2 ) , z = 4 9 ( x 2 + y 2 ) e z = 3 2 + 5 18 ( x 2 + y 2 ) , respectivamente.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8. Esboce o mapa de contorno e o gráfico das seguintes funções:c) f x , y = 2 y - x 2 - y 2
8. Esboce o mapa de contorno e o gráfico das seguintes funções:a) f x , y = x + y 2
8. Esboce o mapa de contorno e o gráfico das seguintes funções:d) f x , y = 6 - x 2 - y 2 ,s ex 2 + y 2 ≤ 4 4 - x 2 + y 2 ,s ex 2 + y 2 ≥ 4
9-Seja z = f x ,y = 24 - 6 x 2 - 2 y 2 3 c)Dê uma parametrização para a curva C do item b .
11-A temperatura num ponto ( x ,y ,z ) é dada por T x ,y ,z = e - x 2 - 2 y 2 + 3 z 2 graus. Identifique a superfície do R 3 cujos pontos possuem temperatura igual à temperatura do ponto - 1 ,- 1 ,1 .