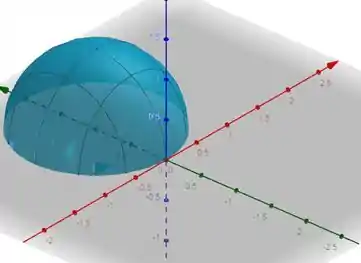
8. Esboce o mapa de contorno e o gráfico das seguintes funções:
c)
Passo 1
Antes de começar, vamos lembrar o que é mapa de contorno/curva de nível. A curva de nivel é a curva descrita quando igualamos a função a uma constante, isto é:
Agora vamos ver como essas curvas se comportam no plano cartesiano:Completando quadrados e multiplicando ambos os termos por , temos:
Desta forma, temos que cada curva de nível é representada por:
Para que a equação faça sentido, temos a condição de que , então .Note que ao elevar ambos os termos ao quadrado para remover a raiz, não perdemos nenhuma curva de nível pois .
Essa curva é uma circunferência de centro e de raio . Sabendo disso, temos que para cada , sua curva de nível é (no exemplo usamos :
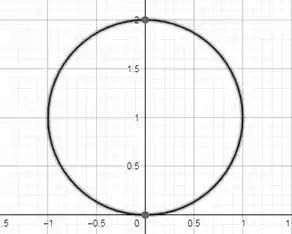
Como as curvas de nível nos ajudam a saber como será o gráfico da função, vamos esboçá-las para alguns valores de (, e conforme diminui, o raio aumenta.
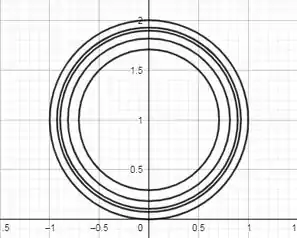
Desenhando cada circunferência em para todo possivel, obtemos o grafico da função, que é:
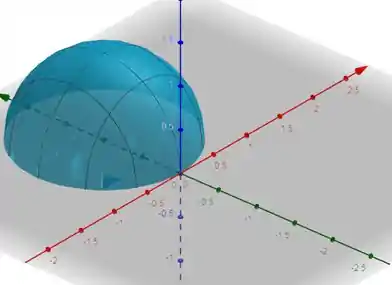
Resposta
Mapa de contorno:
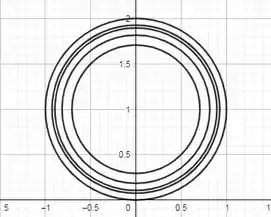
Gráfico: