8. Esboce o mapa de contorno e o gráfico das seguintes funções:
a)
Passo 1
Antes de começar, vamos lembrar o que é mapa de contorno/curva de nível. A curva de nivel é a curva descrita quando igualamos a função a uma constante, isto é:
Agora vamos ver como essas curvas se comportam no plano cartesiano:
Esse gráfico pode ser obtido a partir do gráfico de , seguido de uma reflexão em torno do eixo e depois uma translação de unidades (como no exercício 6). Note que para e , temos que um é a reflexão do outro em relação ao eixo .Sabendo disso, temos que para cada , sua curva de nível é (onde verde representa a curva para e azul representa para :
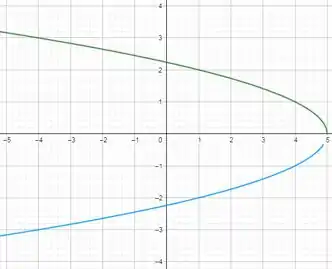
Como as curvas de nível nos ajudam a saber como será o gráfico da função, vamos esboçá-las para alguns valores de (as parábolas têm vértice em ):
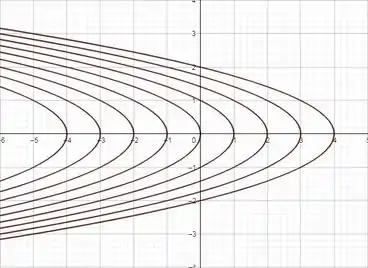
Desenhando cada parábola em para todo possivel, obtemos o grafico da função, que é:
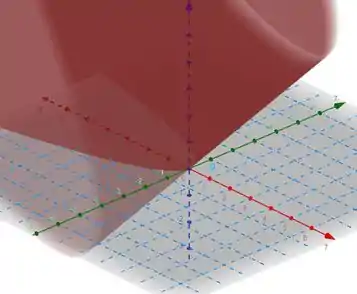
É possível ver que a interseção com o plano resulta em uma parábola, como esperado.
Resposta
Mapa de contorno:
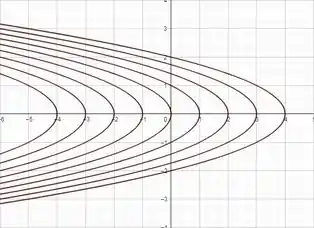
Gráfico:
