Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.1 - Ex. 23
Uma estimativa anual do numero N (em milhões) de assinantes de telefones celulares nos Estados Unidos é mostrada na tabela. (Estimativas dadas para meados do ano).
- Use os dados da tabela para esboçar o gráfico de N como uma função t
- Use seu gráfico para estimar o numero de assinantes de telefones celulares nos anos de 2001 e 2005
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu alguns dados tabelados, para uma estimativa anual do número de assinantes de telefones celulares. Aí ele nos pediu pra usar esses dados e esboçar um gráfico de como uma função do tempo .
Em seguida, nós precisamos usar o gráfico obtido para estimar o número de assinates de celulares em e .
Então, o que nós vamos fazer é marcar os pontos no gráfico cartesiano, com base na tabela que ele nos deu, e depois olhar o valor de quando e quando .
Vamos lá!
Passo 2
Vamos olhar a tabelinha que o enunciado nos deu:
Marcando esses pontos no gráfico cartesiano, com sendo a abscissa (variável independente) e a ordenada (variável dependente), temos:
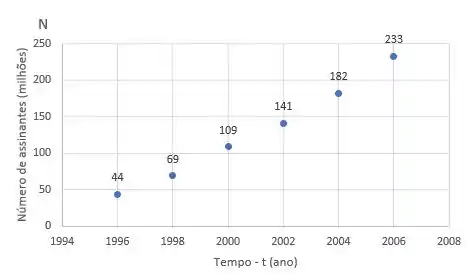
Agora ligando esses pontos, temos a curva de (número de assinates versus tempo):
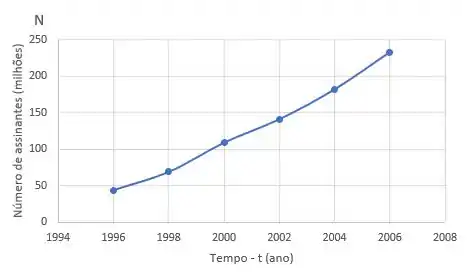
Passo 3
Na letra b) ele diz pra gente usar o gráfico para estimar o numero de assinantes em e . Para fazer isso vamos encontrar os pontos onde e ns curva e obter o valor de correspondente:
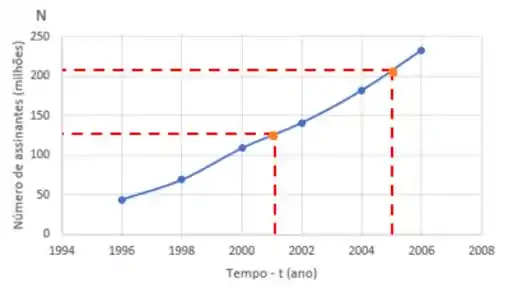
Observe que o primeiro ponto em , corresponde a aproximadamente milhões de assinantes. Além disso, para temos, em , aproximadamente milhões de assinantes.
Prontinho, galera! Até a próxima! 😉