Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 72

Prove que as duas retas:

A 1 x + B 1 y + C 1 = 0                       A 2 x + B 2 y + C 2 = 0

são paralelas se e somente se

A 1 B 2 - A 2 B 1 = 0

Passo 1

Muito toop essa daqui, animados para ver como desembolamos ela?

Então siimbora !!

Neste problema queremos provar que A 1 B 2 = A 2 B 1 quando as Retas 1 e 2 são paralelas.

Para começar, vamos desenhar a situação descrita pelo problema.

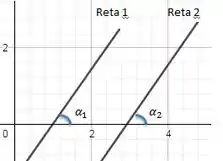
Sabemos que se duas retas são paralelas, elas são equidistantes em toda a sua extensão. E isso só será possível se possuírem a mesma inclinação, certo?

Isso porque se a inclinação delas forem diferentes, eventualmente elas irão se tocar, vale você fazer o teste aí !!

Então:

α 1 = α 2

Consequentemente:

t g   α 1 = t g   α 2

Se lembram como calculamos uma tangente?

Se não lembram, sem problemas !! Eu mostro pra vocês:

t g   α = C a t e t o   O p o s t o C a t e t o   A d j a c e n t e = ∆ y ∆ x = y 1 - y 2 x 1 - x 2

Guardem esta informação no coração de vocês !!

Passo 2

Como vocês viram no Passo 1 precisamos de dois pontos para achar a tangente, ( x 1 ,     y 1 ) e ( x 2 ,     y 2 ) , para as duas retas!!

Para simplificar vamos usar y 1 = x 2 = 0 , ok?

Reta 1: A 1 x + B 1 y + C 1 = 0                

Se y 1 = 0 : A 1 x + C 1 = 0 →   x 1 = - C 1 A 1

Se x 2 = 0 : B 1 y + C 1 = 0 →   y 2 = - C 1 B 1

Substituindo na equação da tangente:

t g   α 1 = y 1 - y 2 x 1 - x 2 = 0 + C 1 B 1 - C 1 A 1 - 0

t g   α 1 = C 1 B 1 . - A 1 C 1 = - A 1 B 1

Reta 2: A 2 x + B 2 y + C 2 = 0

Se y 1 = 0 : A 2 x + C 2 = 0 →   x 1 = - C 2 A 2      

Se x 2 = 0 : B 2 y + C 2 = 0 →   y 2 = - C 2 2

Substituindo na equação da tangente:

t g   α 2 = y 1 - y 2 x 1 - x 2 = 0 + C 2 B 2 - C 2 A 2 - 0

t g   α 2 = C 2 B 2 . - A 2 C 2 = - A 2 B 2

Passo 3

Sabendo os valores das tangentes e sabendo que elas devem ser iguais:

- A 1 B 1 = - A 2 B 2

A 1 B 2 = A 2 B 1

A 1 B 2 - A 2 B 1 = 0

Falei que ia ser legal !!

Resposta

C o m o   v i s t o   a c i m a   ‼

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a equação y = x 2 - 6 x + 8 para responder as questões.Com quais valores de x vale y = 0 Com quais valores de x vale y = - 10 Com quais valores de x vale y ≥ 0 Tera y um valor mínimo? Um valor máx
Seja f x = x + 1 + 4 O domínio natural de f é f 3 f t 2 - 1 f x = 7 se x = A imagem de f é
Os segmentos de retas no plano x y formam letras, conforme o indicadoSe o eixo y for paralelo à letra I, quais das letras representam o gráfico de y = f ( x ) para alguma função de f Se o eixo y é per
Sejam c , l e A comprimento,a largura e a área de um retângulo, respectivamente, e suponha que a largura do retângulo seja a metade do comprimento. (a) Se c for expresso como uma função de l,então c =
A figura dada mostra o gráfico completo dey=f ( x ) . O domínio de f é __________. A imagem de f é __________. f ( - 3 ) = __________. f 1 2 = __________. As soluções de f x = - 3 2 são x = __________