Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 5

(a) Estime a área sob o gráfico de f x = 1 + x ²   de x = - 1 até x = 2 usando três retângulos aproximantes e extremidades direitas. Então, aperfeiçoe sua estimativa utilizando seis retângulos aproximantes. Esboce a curva e os retângulos aproximantes.

(b) Repita a parte (a) usando extremidades esquerdas.

(c) Repita a parte (a) empregando os pontos médios.

(d) De seus esboços das partes (a), (b) e (c), qual parece ser a melhor estimativa?

Passo 1

Eaee, belezinha??

Bom... queremos estimar a área sob o seguinte gráfico:

f x = 1 + x ²  

No intervalo - 1,2 .

Parece complicado?

Para resolver esse problema, devemos utilizar três retângulos aproximantes e extremidades direitas pela formulinha:

A = ∑ i = 1 n f x i ∆ x ,     ∆ x = b - a n ,     x i = a + i ∆ x

Em seguida, devemos aperfeiçoar a estimativa utilizando seis retângulos aproximantes.

Depois a gente deve fazer a mesma coisa para extremidades esquerdas e pontos médios!!

Para extremidades esquerdas, i começar em 0 em A e nos pontos médios x i recebe uma nova formula:

x i = a + i ∆ x 2

E aí?? Bora lá!! 😉

Passo 2

Para f x = 1 + x ² e aproximação com três retângulos temos ∆ x = 2 - - 1 3 = 1 , logo, pela formulinha do passo 1:

R 3 = ∑ i = 1 n f x i ∆ x = f x 1 + f x 2 + f x 3 ∆ x

Para definir os pontos x i , usamos a formulinha:

x i = a + i ∆ x

x 1 = - 1 + 1 1 = 0

x 2 = - 1 + 2 1 = 1

x 3 = - 1 + 3 1 = 2

Logo:

R 3 = f 0 + f 1 + f 2 1

R 3 = 1 + 2 + 5

R 3 = 8

Temos o seguinte gráfico com R 3 :

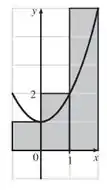
Tranquilo até aqui?

Passo 3

Para f x = 1 + x ² e aproximação com seis retângulos temos ∆ x = 2 - - 1 6 = 1 2 , logo, pela fórmula da área que vimos no passo 1:

R 6 = ∑ i = 1 n f x i ∆ x = 0,5 f x 1 + f x 2 + f x 3 + f x 4 + f x 5 + f x 6

Definindo os valores de x i da mesma forma que fizemos no passo anterior, vamos chegar em:

R 6 = 0,5 f - 0,5 + f 0 + f 0,5 + f 1 + f 1,5 + f 2

R 6 = 0,5 1,25 + 1 + 1,25 + 2 + 3,25 + 5

R 6 = 0,5 13,75

R 6 = 6,875

Temos o seguinte gráfico com R 6 :

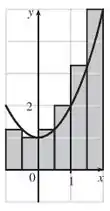
Agora vamos fazer para a extremidade esquerda!!

Show?

Passo 4

Para 3 retângulos aproximantes e utilizando a extremidade esquerda, já vimos que para 3 retângulos ∆ x = 1 .

Além disso, como estamos nos aproximando pela esquerda, nosso somatório começa em i = 0 .

A = ∑ i = 0 n f x i ∆ x ,     ∆ x = b - a n ,     x i = a + i ∆ x

Ou seja:

x 1 = - 1 + 0 1 = - 1

x 2 = - 1 + 1 1 = 0

x 3 = - 1 + 2 1 = 1

Assim o somatório fica:

L 3 = 1 f - 1 + f 0 + f 1

L 3 = 2 + 1 + 2

L 3 = 5

O gráfico é o seguinte:

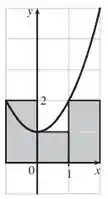
Estamos quase no fim!

Passo 5

Agora vamos aperfeiçoar para 6 retângulos aproximantes!!

Repetindo os processos que fizemos anteriormente...

L 6 = 0,5 f - 1 + f - 0,5 + f 0 + f 0,5 + f 1 + f 1,5

L 6 = 0,5 2 + 1,25 + 1 + 1,25 + 2 + 3,25

L 6 = 5,375

Assim, o gráfico é o seguinte:

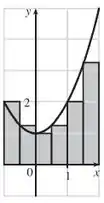
Agora vamos fazer para os pontos médios!! 😉

Passo 6

Por fim, para o ponto médio e 3 retângulos aproximantes.

Para os pontos médios, temos:

x i = - a + i ∆ x 2

Portanto, o somatório nesse caso, fica:

M 3 = 1 f - 0,5 + f 0,5 + f 1,5

M 3 = 1,25 + 1,25 + 3,25

M 3 = 5,75

Assim, temos o seguinte gráfico:

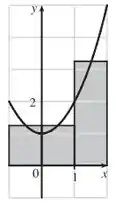
Maravilha!

Passo 7

Aperfeiçoando para 6 retângulos aproximantes, temos:

M 6 = 0,5 f - 0,75 + f - 0,25 + f 0,25 + f 0,75 + f 1,25 + f 1,75

M 6 = 0,5 1,5625 + 1,0625 + 1,0625 + 1,5625 + 2,5626 + 2,0625

M 6 = 5,9375

Assim, temos o seguinte gráfico:

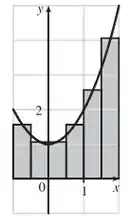
A melhor estimativa parece ser M 6 pois sé a que mais se aproxima da curva sob o gráfico!! 😉

O que acha? Responde Aí!

Resposta

  1. R 3 = 8 e R 6 = 6,875
  2. L 3 = 5 e L 6 = 5,375
  3. M 3 = 5,75 e M 6 = 5,9375
  4. M 6
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse a integral como um limite de somas. Não calcule o limite. 29 . ∫ 2 6 x 1 + x 5 d x
Expresse a integral como um limite de somas. Depois, calcule, usando um sistema de computação álgébrica para encontrar a soma e o limite. 31 . ∫ 0 π sen ⁡ 5 x d x
28. Demonstre que ∫ a b x 2 d x = b 3 - a 3 2 .
Expresse a integral como um limite de somas. Depois, calcule, usando um sistema de computação algébrica para encontrar a soma e o limite.∫ 2 10 x 6 d x
Demonstre que: ∫ a b x d x = b 2 - a 2 2