Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 34
Use o cálculo para encontrar a área do triângulo com os vértices dados.
Passo 1
Bom galera, nesse exercício queremos encontrar a área do triângulo especificado.Com os seguintes vértices:
Vamos desenhar no plano cartesiano pra ficar mais claro:
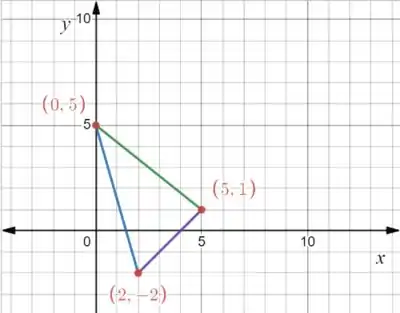
A área delimitada por essas retas podem ser calculadas por:
O problema é que aqui temos retas, então vamos ter que dividir esse triangulo assim:
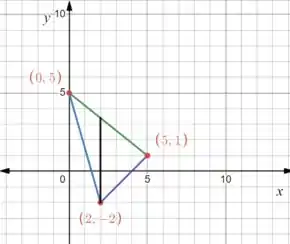
Então vamos calcular a área de cada metade e depois somar! Mas antes disso precisamos das equações das retas!
Passo 2
Com dois pontos, podemos encontrar uma equação da reta utilizando a seguinte fórmula
E
Dessa forma, entre os pontos e temos a seguinte equação:
Entre os pontos e temos a seguinte equação:
Entre os pontos e temos a seguinte equação:
Passo 3
Então pra área a esquerda podemos fazer:
O limite de integração inferior vai ser , que é onde as retas se interceptam e o limite de integração superior vai ser na intercepção das retas com a reta . Então temos:
Integrando:
Aplicando os limites de integração:
Passo 4
Agora a área da direita:
O limite de integração inferior vai ser , que é onde as retas se interceptam e o limite de integração superior vai ser na intercepção das retas com a reta . Então temos:
Agora somamos as duas áreas: