Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 7.7 - Ex. 29

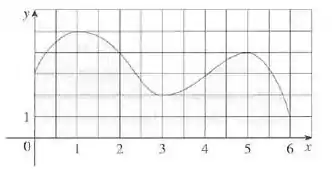
Estime a área sob o gráfico na figura usando (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson, cada qual com n = 6 .

Passo 1

  1. Temos o intervalo 0 ≤ x ≤ 6 , e vamos usar n = 6 , temos que ∆ x :

    2. ∆ x = b - a n = 6 - 0 6 = 1

    Para achar a aproximação pela Regra do Trapézio fazemos uma média das aproximações da soma de Riemann, com a fórmula:

    T n = 1 2 ∆ x f x 0 + 2 f x 1 + 2 f x 2 + ∙ ∙ ∙ + 2 f x n - 1 + f x n

    A = T 6 = 1 2 ∆ x f 0 + 2 f 1 + 2 f 2 + 2 f 3 + 2 f 4 + 2 f 5 + f 6 = 1 2 ∙ 1 3 + 2.5 + 2.4 + 2.2 + 2.2,8 + 2.4 + 1 = 19,8

    Passo 2

  2. Agora vamos achar a aproximação do ponto médio M 6 , onde os x dos pontos são os pontos médios de cada intervalo:

    3. M n = ∑ i = 1 n f x i - ∆ x = f x - 1 + f x - 2 + f x - 3 ∙ ∙ ∙ + f x - n ∆ x

    A = M 6 = ∑ i = 1 n f x i - ∆ x = f 0,5 + f 1,5 + f 2,5 + f 3,5 + f 4,5 + f 5,5 1 = 4,5 + 4,7 + 2,6 + 2,2 + 3,4 + 3,2 = 20,6

    Passo 3

  3. Com a Regra de Simpson é usado parábolas ao invés de segmentos de reta para aproximar a curva, assim a fórmula fica com um padrão 1 , 4 , 2 , 4 , 2 , . . . , 4 , 2 , 4 , 1 :

A = S n = f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + ∙ ∙ ∙ + 2 f x n - 2 + 4 f x n - 1 + f x n ∆ x 3

S 6 = f 0 + 4 f 1 + 2 f 2 + 4 f 3 + 2 f 4 + 4 f 5 + f 6 ∆ x 3 = 3 + 4.5 + 2.4 + 4.2 + 2.2,8 + 4.4 + 1 1 3 . 1 = 20,5 3 -

Resposta

  1. A = T 6 = 19,8
  2. A = M 6 = 20,6
  3. A = S 6 = 20,5 3 -
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as aproximações T 10 , M 10 e S 10 para a integral ∫ 0 π sen ⁡ x d x e os erros correspondentes E T , E M e E S .Compare os erros reais na parte (a) com as estimativas de erro dadas por ( 3 )
Ache as aproximações T 10 e M 10 para ∫ 1 2 e 1 x d x .Estime os erros envolvidos nas aproximações na parte (a).Que tamanho de n devemos escolher para que as aproximações T n e M n para a integral na
Calcule as aproximações L n , R n , T n e M n para n = 5 , 10 e 20 . Então calcule os erros correspondentes E L , E R , E T e E M . (Arredonde seus resultados para seis casas decimais. Você pode usar
Calcule as aproximações L n , R n , T n e M n para n = 5 , 10 e 20 . Então calcule os erros correspondentes E L , E R , E T e E M . (Arredonde seus resultados para seis casas decimais. Você pode usar
O gráfico da aceleração a t de um carro, medida em m/s², é mostrado. Use a Regra de Simpson para estimar o aumento da velocidade do carro durante o intervalo de 6 segundos.