Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.7 - Ex. 35
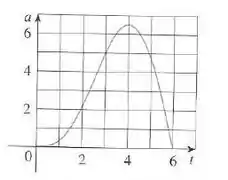
O gráfico da aceleração de um carro, medida em m/s², é mostrado. Use a Regra de Simpson para estimar o aumento da velocidade do carro durante o intervalo de segundos.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente estimar o aumento da velocidade do carro durante o intervalo de segundos. Pra isso, ele nos deu o gráfico da aceleração do carro, medida em m/s².
Olhando para o gráfico, a gente percebe que o intervalo considerado vai de zero até segundos, ou seja:
Então, vamos considerar também medições da aceleração. Assim, temos e a variação das medições será dada por:
Onde e são extremos do intervalo . Depois disso, basta a gente aplicar a fórmula de Simpson:
Considerando que seja o aumento de velocidade desejado e as medições de aceleração oferecidas pela tabela.
Vamos lá!
Passo 2
Temos o intervalo , e vamos usar . Então, o nosso será:
Com a Regra de Simpson é usado parábolas ao invés de segmentos de reta para aproximar a curva, assim a fórmula fica com um padrão , , , , . . . , , , , :
Então, estimamos a integral na forma:
De modo que:
E calculando, temos a velocidade:
Portanto, o aumento da velocidade estimado do carro durante o intervalo de segundos é de .
Valeu, galera! Até a próxima! 😉