Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.3 - Ex. 35
As taxas para despachar cargas por navios são frequentemente baseadas em fórmulas que oferecem u preço menor por quilo quando o tamanho da carga é maior. Suponha que quilos sejam o peso de uma carga, seja o seu custo total e
Faça um esboço do gráfico de . Ache cada um dos seguintes limites
Passo 1
Letra
Vamos começar fazendo um esboço de . Para isso temos que entender um pouquinho só como é essa nossa
O enunciado disse que
Então temos uma reta de até , outra reta de até , terminando com outra reta a partir de
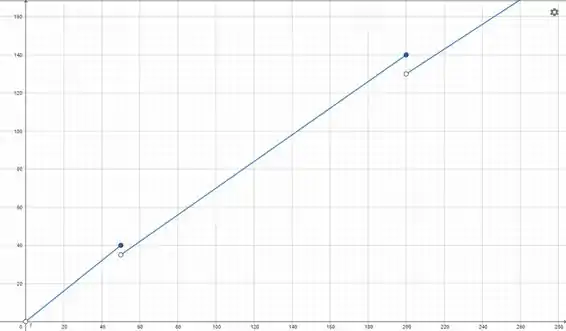
Para fazer esse gráfico, devemos fazer a reta de até , e colocar aquela bola aberta em e fechada em . Isso porque ele fala que é maior que e menor ou igual a .
depois devemos fazer a reta de até , e colocar aquela bola aberta em e fechada em . Isso porque ele fala que é maior que e menor ou igual a .
Por fim, devemos fazer a reta a partir de , deixando bola aberta em porque ele fala de valores de maiores que .
O gráfico vai ficar
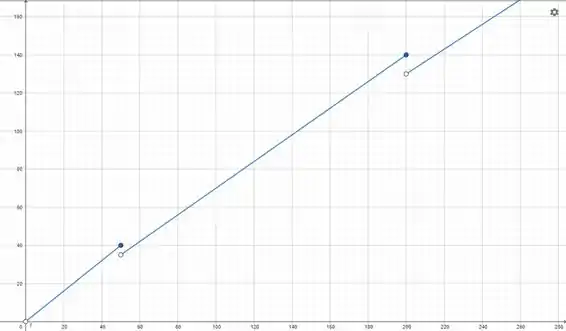
Passo 2
Letra
Ele quer o limite de
Esse é o limite pela esquerda. Para isso, temos que pegar a expressão da função para valores menores que .
Aqui vai ser .
Logo, vamos ter
Passo 3
Letra
Ele quer o limite de
Esse é o limite pela direita. Para isso, temos que pegar a expressão da função para valores maiores que . Mas cuidado, tem duas expressões maiores que . A que vamos escolher é aquela logo depois do .
Aqui vai ser .
Logo, vamos ter
Passo 4
Letra
Ele quer o limite de
Esse é o limite pela esquerda. Para isso, temos que pegar a expressão da função para valores menores que . Mas cuidado, tem duas expressões menores que . A que vamos escolher é aquela logo antes do .
Aqui vai ser .
Logo, vamos ter
Passo 5
Letra
Ele quer o limite de
Esse é o limite pela direita. Para isso, temos que pegar a expressão da função para valores maiores que
Aqui vai ser .
Logo, vamos ter
Resposta
