Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 47
- Estime o valor do limite
Com 5 casas decimais. Esse número lhe parece familiar?
- Confirme sua resposta da letra (a) fazendo o gráfico da função.
Com 5 casas decimais. Esse número lhe parece familiar?
Passo 1
Falaee, belezinha?? Bom... queremos estimar o valor do seguinte limite:
Para isso, devemos aplicar valores que se aproximem de .
Depois, devemos plotar o gráfico de para confirmar a nossa estimativa.
Agora vamos lá!! 😉
Passo 2
- Seja
Calcularemos o valor do limite fazendo uma tabela de valores de confrontando quando pela direita e pela esquerda.
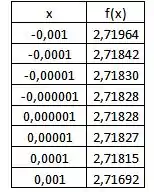
Pela tabela, podemos ver que
E esse valor é aproximadamente o valor de (Numero de Euler)
Passo 3
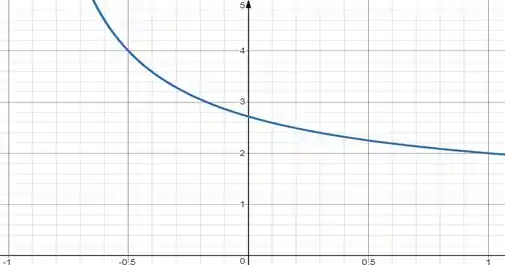
Perceba que, analisando o gráfico, a curva cruza o eixo em .
Entendeu direitinho?? Responde aee 😉
Resposta
Exercícios de Livros Relacionados
De que tamanho devemos tomar x para que 1 x 20,0001 Tomando r = 2 no Teorema 5, temos a igualdade lim x → ∞ 1 x 2 = 0 Demonstre isso diretamente usando a Definição 7
Use a definição 8 para demonstrar que lim x → - ∞ 1 x = 0
Demonstre que lim x → ∞ f ( x ) = lim t → 0 + f 1 t E lim x → - ∞ f ( x ) = lim t → 0 - f 1 t Se esses limites existirem
Calcule lim x → ∞ senh x e x .
Se uma onda de comprimento L se move à velocidade v em um corpo de água de profundidade d , então v = g L 2 π tgh 2 π d L em que g é a aceleração da gravidade. (Veja a Figura 5.) Explique por que a