Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.11 - Ex. 49
Se uma onda de comprimento se move à velocidade em um corpo de água de profundidade , então
em que é a aceleração da gravidade. (Veja a Figura 5.) Explique por que a aproximação
é adequada para águas profundas.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente explicar porque é uma boa aproximação para a velocidade de uma onda de comprimento se movendo em águas profundas. Sabendo que representa essa profundidade e que a equação geral dessa velocidade é dada por:
Nesse caso, precisamos analisar o comportamento da função à medida que a profundidade aumenta e verificar se essa é realmente uma boa aproximação.
Vamos lá!
Passo 2
Primeiro vamos analisar e depois o comportamento de .
Podemos perceber que a medida que cresce, também cresce.
Além disso, olhando o gráfico da tangente hiperbólica de , nós notamos que à medida que cresce, se aproxima de . Olha só:
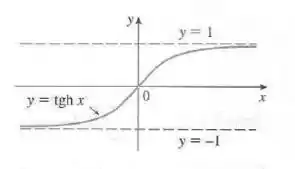
Isso é válido inclusive para .
Então, à medida que o argumento da função tangente hiperbólica tende para infinito (), porque a profundidade aumenta indefinidamente, essa função tende a ().
Dessa forma, podemos fazer a aproximação:
Valeu, galera! Até a próxima! 😉
Resposta
A aproximação é adequada porque à medida que , .