- Estime o volume do sólido que está abaixo da superfície e acima do retângulo
Utilize a soma de Riemann com , e tome como ponto amostral o canto superior direito de cada sub-retângulo.
- Use a Regra do Ponto Médio para estimar o volume do sólido da parte (a).
Utilize a soma de Riemann com , e tome como ponto amostral o canto superior direito de cada sub-retângulo.
Passo 1
Fala, pessoal! Tudo certinho??
Nessa questão vamos estimar o volume de um sólido usando soma de Riemann, com e .
Relembrando que a soma de Riemann é dada por essa fórmula aqui:
A diferença da letra (a) para a letra (b) é o ponto amostral , ou seja, o ponto que vamos calcular para cada :
Na letra (a), vamos usar o ponto no canto superior direito de cada sub-retângulo.
Na letra (b), vamos usar o ponto no meio de cada sub-retângulo.
Então vamos às contas!
Passo 2
-
Como vemos na fórmula da soma de Riemann:
O valor de equivale a quantidade de partições que vamos ter em , e são as partições em , então, o nosso domínio vai ser dividido assim:
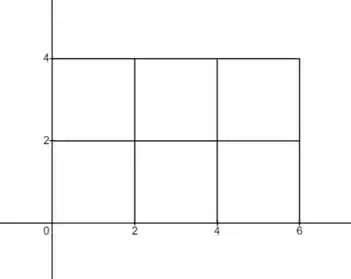
Temos que a superfície é o gráfico de e vamos ter que é a área de cada retângulo, então , e que e , então usando a soma de Riemann para estimar o volume temos:
Onde os pontos são os cantos superiores direito de cada sub-retângulo.
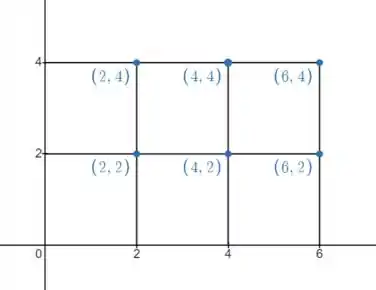
Assim,
Ou seja,
Passo 3
Agora para usar a regra do ponto médio, vamos considerar que os pontos amostrais serão:
O domínio e as partições que vamos usar são os mesmos, então continuamos com .
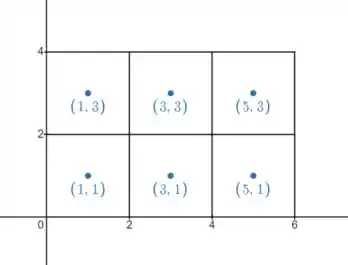
Logo,