Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 16.4 - Ex. 1 e

Estude a função dada com relação a máximo e mínimo no conjunto dado.

e) f x ,   y = y 2 - x 2     em A = { x ,   y   ∈   R 2 ; x 2 + y 2 ≤ 4 } .

Passo 1

Vamos calcular as derivadas para analisar os pontos críticos.

∂ f ∂ x = - 2 x

∂ f ∂ y = 2 y

Encontrando os pontos críticos,

∂ f ∂ x = ∂ f ∂ y = 0  

- 2 x = 0 2 y = 0

Resolvendo o sistema

  x = 0

y = 0

p = ( 0,0 ) é ponto crítico. Aplicando em f

f 0,0 = 0

Passo 2

Vejamos agora a representação da fronteira,

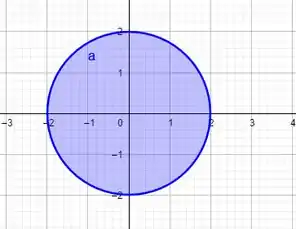
Para facilitar nossas contas, vamos fazer a parametrização, x = 2 c o s t e   y = 2 s e n t

f t = 4 s e n 2 t - 4 cos 2 ⁡ t = - 4 cos 2 ⁡ t - s e n 2 t = - 4 cos ⁡ 2 t

Vamos encontrar os pontos críticos de f ,

f ' t = 8 s e n ( 2 t )

Igualando a zero,

f ' t = 0  

8 s e n 2 t = 0 → s e n 2 t = 0

Resolvendo a equação, temos que:

t = 0 ,   t = π 2 ,   t = π , t = 3 π 2

Para t = 0 → x = 2 cos ⁡ 0 = 2 e y = 2 s e n 0 = 0 , temos o ponto P 1 = ( 2,0 ) . Jogando na função temos que f P 1 = - 4 .

Para t = π / 2 → x = 2 cos ⁡ π / 2 = 0 e y = 2 s e n π / 2 = 2 , temos o ponto P 2 = ( 0 , 2 ) . Jogando na função temos que f P 2 = 4 .

Para t = π → x = 2 cos ⁡ π = - 2 e y = 2 s e n π = 0 , temos o ponto P 3 = ( - 2,0 ) . Jogando na função temos que f P 3 = - 4 .

Para t = 3 π / 2 → x = 2 cos ⁡ 3 π / 2 = 0 e y = 2 s e n 3 π / 2 = - 1 , temos o ponto P 4 = ( 0 , - 2 ) . Jogando na função temos que f P 4 = 4 .

Então concluímos que

f 0,2 = f 0 , - 2 = 4 são máximos

f 2,0 = f - 2,0 = - 4 são mínimos

e o ponto que achamos no passo 1 não entra na história por que ele é intermediário dos pontos acima

Resposta

0 , - 2 e 0,2 são máximos

( - 2,0 ) e 2,0 são mínimos

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os máximos, minimos e pontos de sela de f ( x , y ) , se existirem, dadosa. f x = 2 x - 4 y e f y = 2 y - 4 x b. f x = 2 x - 2 e f y = 2 y - 4 c. f x = 9 x 2 - 9 e f y = 2 y + 4 Descreva seu
Considere a função ƒ(x, y) = x2 + y2 + 2xy – x – y + 1 sobre oquadrado 0 ≤ x ≤ 1 e 0 ≤ y ≤ 1.a. Mostre que ƒ tem um mínimo absoluto ao longo do segmento de reta 2x + 2y = 1 nesse quadrado. Qual é o va
Como você encontra os extremos de uma função contínua ƒ(x, y)em uma região limitada fechada no plano xy? Dê um exemplo.
Como você define máximo local, mínimo local e pontos desela para uma função diferenciável ƒ(x, y)? Dê exemplos
Nos Exercícios 31-38, encontre os máximos e mínimos absolutos das funções nos domínios dados. f x ,y = 2 x 2 - 4 x + y 2 - 4 y + 1 na placa triangular fechada e limitada pelas retas x = 0 , y = 2 , y