Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 16.4 - Ex. 1 d
Estude a função dada com relação a máximo e mínimo no conjunto dado.
d) em e
Passo 1
Vamos calcular as derivadas para analisar os pontos críticos.
Temos que é ponto crítico e aplicando
Passo 2
Vejamos agora a representação da fronteira,
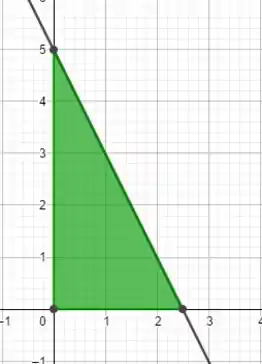
Aplicando , temos
Passo 3
Vamos tentar mais uma coisinha.
Isolando da definição de A,
Como para valores dentro do intervalo , assume valores positivos (crescente). E para valores dentro do intervalo , irá assumir valores negativos (decrescente) temos que é um ponto de máximo no intervalo para
Dai,
Logo , é ponto de máximo.
Resposta
é ponto de máximo.
Exercícios de Livros Relacionados
Mostre que (0, 0) é um ponto crítico de ƒ(x, y) = x2 + kxy + y2,não importando qual o valor da constante k. (Sugestão: considere dois casos: k = 0 e k Z 0.)
O discriminante f x x f y y - f x y2 é zero na origem para cada uma das funções a seguir, de modo que o teste da derivada de segunda ordem falha. Determine se a função tem um máximo, um mínimo ou nenh
Funções:a. f ( x , y ) = x 2 + y 2 b. g ( x , y ) = 1 / x 2 + y 2 Curvas:i) A reta x = t ,y = 2 - 2 t ii) O segmento de reta x = t ,y = 2 - 2 t ,0 ≤ t ≤ t .
Funções:a. f ( x , y ) = x + y b. g ( x , y ) = x y c. h ( x , y ) = 2 x 2 + y 2 Curvas:i) O semicírculo x 2 + y 2 = 4 ,y ≥ 0 .ii) O quarto de circunferência x 2 + y 2 = 4 ,x ≥ 0 ,y ≥ 0 Utilize as equ
Encontre dois números a e b c o m a ≤ b , tais que ∫ a b 24 - 2 x - x 2 1 / 3 d x tenha seu valor máximo.