Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 100d
No estudo de penetração do congelamento descobriu-se que a temperatura no instante (medido em dias) a uma profundidade (medida em metros) pode ser modelada pela função:
Onde e é uma constante positiva.
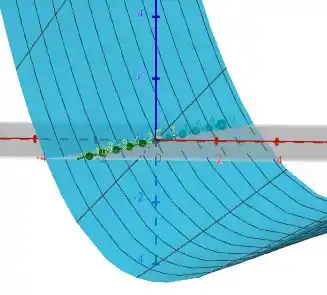
d) Se , e , use um computador para traçar o gráfico de .
Passo 1
Com os valores dados pelo enunciado, nossa função ficará da seguinte forma:
Plotando o gráfico obteremos algo parecido com:
Resposta
Exercícios de Livros Relacionados
Equação do calor Uma equação diferencial parcial importante que descreve a distribuição do calor em uma região no tempo t pode ser representada pela equação do calor unidimensionalMostre que u ( x ,t
Nos Exercícios 1-3, comece desenhando um diagrama que mostre as relações entre as variáveis.2. Se w = x 2 + y - z + s e ny e x + y = t encontre: a . δ w δ y x , z
Variação das dimensões de uma caixa. Os comprimentos a , b e c das arestas de uma caixa retangular variam com o tempo. No instante em questão, a = 1m , b = 2m , c = 3m , d a / d t = d b / d t = 1m / s
Mostre que cada função dos Exercícios 73-80 satisfaz uma equação de Laplace.
Mostre que cada função dos Exercícios 73-80 satisfaz uma equação de Laplace.