Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.4 - Ex. 42

Variação das dimensões de uma caixa. Os comprimentos a , b e c das arestas de uma caixa retangular variam com o tempo. No instante em questão, a = 1   m , b = 2   m , c = 3   m , d a / d t = d b / d t = 1   m / s e d c / d t = - 3   m / s . A quais taxas o volume V e a área S da caixa variam nesse instante? As diagonais do interior da caixa estão aumentando ou diminuindo de comprimento?

Passo 1

Olá galerinha, vem comigo!! Com os dados do enunciado, sabemos que temos uma caixa da seguinte maneira:

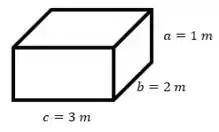
Para a taxa de variação do volume, temos a seguinte equação:

∂ V ∂ t = ∂ V ∂ a d a d t + ∂ V ∂ b d b d t + ∂ V ∂ c d c d t

Os valores de d a / d t , d b / d t e d c / d t temos através do enunciado, e as derivadas ∂ V / ∂ a , ∂ V / ∂ b e ∂ V / ∂ c , conseguimos obter pela equação do volume, que é:

V = a ∙ b ∙ c

Logo:

∂ V ∂ a = b c = 2 ∙ 3 = 6   m 2 ∂ V ∂ b = a c = 1 ∙ 3 = 3   m 2 ∂ V ∂ c = a b = 1 ∙ 2 = 2   m 2

Substituindo os valores na equação de ∂ V / ∂ t :

∂ V ∂ t = 6   m 2 ∙ 1   m / s + 3   m 2 ∙ 1   m / s + 2   m 2 ∙ ( - 3   m / s )

= 6   m 3 / s + 3   m 3 / s - 6   m 3 / s

∂ V ∂ t = 3   m 3 / s

Passo 2

Agora vamos calcular a taxa da área S , iremos fazer a mesma coisa que foi feito para o volume. A equação da área total, é:

S = 2 a b + 2 a c + 2 b c

As derivadas de a , b e c :

∂ S ∂ a = 2 b + 2 c = 2 b + c = 2 ∙ 2 + 3 = 10   m ∂ S ∂ b = 2 a + 2 c = 2 a + c = 2 ∙ 1 + 3 = 8   m ∂ S ∂ c = 2 a + 2 b = 2 a + b = 2 ∙ 1 + 2 = 6   m

A equação da variação da área, é dada por:

∂ S ∂ t = ∂ S ∂ a d a d t + ∂ S ∂ b d b d t + ∂ S ∂ c d c d t

Substituindo os valores:

∂ S ∂ t = 10   m ∙ 1   m / s + 8   m ∙ 1   m / s + 6   m ∙ ( - 3   m / s )

= 10   m 2 / s + 8   m 2 / s - 18   m 2 / s

∂ S ∂ t = 0

Passo 3

Para descobrirmos se as diagonais no interior da caixa estão aumentando ou diminuindo de comprimento, precisamos da equação da diagonal:

D = a 2 + b 2 + c 2 = 1 2 + 2 2 + 3 2

D = 3,74   m

As derivadas são:

∂ D ∂ a = a a 2 + b 2 + c 2 = 1 3,74 = 0,27 ∂ D ∂ b = b a 2 + b 2 + c 2 = 2 3,74 = 0,53 ∂ D ∂ c = c a 2 + b 2 + c 2 = 3 3,74 = 0,80

Então:

∂ D ∂ t = ∂ D ∂ a d a d t + ∂ D ∂ b d b d t + ∂ D ∂ c d c d t

∂ D ∂ t = 0,27 ∙ 1   m / s + 0,53 ∙ 1   m / s + 0,80 ∙ ( - 3   m / s )

= 0,27   m / s + 0,53   m / s - 2,40   m / s

∂ S ∂ t = - 1,60   m / s

Como o valor encontrado é menor que o inicial, então podemos dizer que as diagonais do interior da caixa estão diminuindo de comprimento.

Tchau galerinha, até mais!!

Resposta

  • ∂ V ∂ t = 3   m 3 / s

  • ∂ S ∂ t = 0

  • As diagonais estão diminuindo.

Exercícios de Livros Relacionados

Mostre que as funções nos Exercícios 81-87 são todas soluções da equação de onda.
Nos Exercícios 35-40, encontre a derivada parcial da função em relação a cada variável.
Nos Exercícios 23-34, encontre f_x , f_y . f_z .
Nos Exercícios 35-40, encontre a derivada parcial da função em relação a cada variável.
Mostre que as funções nos Exercícios 81-87 são todas soluções da equação de onda.