Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.2 - Ex. 6
Dê exemplo de funções e tais que , e
Passo 1
Para que tenhamos devemos considerar:
Passo 2
Então vamos pensar em duas funções e tal que , . Nós podemos escolher quaisquer pares de funções em que sabemos que o limites quando tende para o infinito o valor da função também vai para infinito, também precisamos tomar cuidado para que , ok?
Temos que ter que quando está indo para o infinito, o também vai.
Então podemos pensar por exemplo em uma reta crescente ou uma parábola com a concavidade para cima, certo? Porque olha: o gráfico das duas vai para o infinito quando também vai:
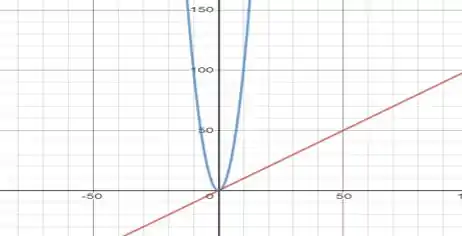
Então, se pegarmos e , estaremos cumprindo com os nossos dois primeiros requisitos:
Agora vamos ver se nossa escolha também cumpre o terceiro, requisito que é:
Substituindo nossas funções escolhidas no cálculo do limite, teremos:
Ao calcular esse nosso novo limite, vemos que temos um polinômio onde termo de maior grau é o , e por ser o termo de maior grau em um limite onde tende ao infinito seu valor vai predominar no resultado do limite, pois ele vai para o infinito mais rápido que os outros termos. Mas repare que ele é negativo, então:
Como isso, comprovamos que
Comprovando que as funções e são boas escolhas.
Resposta