Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.2 - Ex. 8
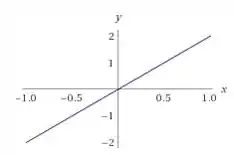
Dê exemplo (por meio de um gráfico) de uma função , definida e derivável em , tal que para todo .
Passo 1
Bom, o melhor exemplo de uma função definida e derivável e que tenha derivada sempre positiva é uma função de primeiro grau. Ou seja, uma reta com coeficiente angular positivo.
A equação de uma reta pode ser dada por:
Onde é o coeficiente angular: ele determina se a reta é crescente ou decrescente . E o coeficiente é chamado de coeficiente linear: ele nos diz onde a reta cruza o eixo dos .
Passo 2
Sendo assim, vou escolher uma reta com e :
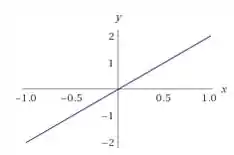
Resposta
Exercícios de Livros Relacionados
Faça o gráfico de y = 3 x 2 em uma janela que contenha - 2x2 , 0 y3 . Em seguida, na mesma tela, faça o gráfico de y = x + h 3 - x 3 h para h=2 ;1 ;0,2 . Então tente h=- 2 ;- 1 ;- 0,2 . Explique o que
63. Se f ´ ( a ) existe, prove que f ´ a = lim ∆ x → 0 f a + ∆ x - f ( a - ∆ x ) 2 ∆ x
62. Use a fórmula do Exercício 61 para encontrar f ´ ´ x se f x = a x .
61. Se f ´ ´ x = lim ∆ x → 0 f ´ x + ∆ x - f ´ ( x ) ∆ x ache f ´ ´ ( x ) se f x = a x 2 + b x .
64. Seja f uma função cujo domínio seja o conjunto de todos os números reais e f a + b = f a . f ( b ) para todo aeb . Além disso, suponha que f 0 = 1ef ´ 0e x i s t a .Prove que f ( x ) existe para t