Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.11 - Ex. 1
No exemplo 1, o peru é removido do forno quando sua temperatura atinge 185° F e colocado sobre uma mesa em uma sala onde a temperatura é de 75° F. Após dez minutos a temperatura é de 172° F, e após 20 minutos, 160° F. Use uma aproximação linear para predizer a temperatura do peru após meia hora. Você acha sua predição superestimada ou subestimada? Por quê?
Passo 1
Se é uma função que diz a temperatura no tempo , vamos utilizar uma aproximação linear para calcular a temperatura para minutos. A fórmula para a aproximação linear é:
Sendo um ponto que tomamos como referência e o ponto no qual queremos aproximar a função . Usando o tempo de 20 minutos como referência, nossa aproximação então vai ficar assim:
Passo 2
Agora precisamos de uma aproximação para a derivada da temperatura em relação ao tempo em 20 minutos, . Vamos esboçar rapidamente um gráfico da temperatura:
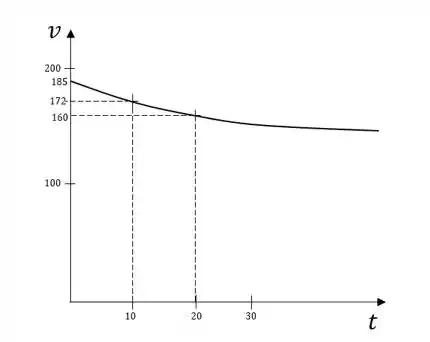
Podemos aproximar pela taxa de variação média da temperatuera entre 10 e 20 minutos:
Então:
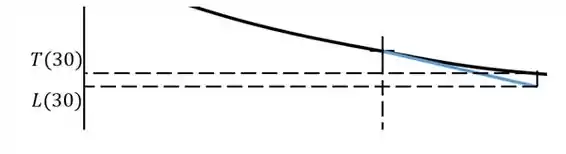
Esse resultado é subestimado, pois consideramos que a inclinação da curva entre 20 e 30 min é constante a mesma que a inclinação média entre 10 e 20 minutos. O que acontece na verdade é que a inclinação da curva está diminuindo. A figura mostra como estamos subestimando o resultado:
