Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.4 - Ex. 37

No exercício abaixo, realize uma divisão longa no integrando, escreva a fração própria como soma de frações parciais e então calcule a integral.

37 –

∫ y 4 + y 2 - 1 y 3 + y d x

Passo 1

No primeiro passo realizaremos a divisão de polinômios:

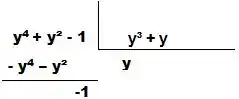
Assim temos:

∫ y - 1 y 3 + y d x

Colocando y em evidência, tomamos que:

y 3 + y = y ( y 2 + 1 )

Analisando o polinômio vimos que o seu maior grau é o 3, logo terá 3 letras para substituição, porém o coeficiente y 2 + 1 é irredutível, assim teremos que esy-crever nossa fração da seguinte forma:

1 y ( y 2 + 1 ) = A y + B y + C y 2 + 1

Agora tiramos o mínimo múltiplo comum da operação, observe:

1 y ( y 2 + 1 ) = A y 2 + 1 + y ( B y + C ) y ( y 2 + 1 )

Podemos cortar os denominadores:

1 = A y 2 + 1 + y ( B y + C )

Aplicando a multiplicação distributiva:

1 = A y 2 + A + B y 2 + C y

Organizando os fatores comuns:

1 = A + B y 2 + C y + A

Observamos que a possui apenas a constante, que podemos representar da seguinte forma:

0 y 2 + 0 y + 1 =   A + B y 2 + C y + A

Desta forma:

A + B = 0

C = 0

A = 1

Como descobrimos A, vamos achar B agora:

1 + B = 0 ; B = - 1

Substituindo A, B e C na fração, temos:

1 y ( y 2 + 1 ) = 1 y + - 1 y + 0 y 2 + 1 = 1 y - y y 2 + 1

Passo 2

Agora vamos substituir na Integral:

∫ y - 1 y - y y 2 + 1 d y =   ∫ y   d y - ∫ 1 y   d y + ∫ y y 2 + 1 d y

Resolvendo a primeira integral temos:

∫ y   d y = y 2 2

Resolvendo a segunda integral:

- ∫ 1 y   d y =   - ln ⁡ y

Resolvendo a terceira integral:

∫ y y 2 + 1 d y

Utilizaremos o método de substituição:

u = y 2 + 1

d u = 2 y

d y = 1 d u = 1 2 y

Assim: para u = y 2 + 1

∫ y u ⋅ 1 2 y   d u = 1 2 ∫ 1 u d u = 1 2 ln ⁡ u = 1 2 ln ⁡ y 2 + 1  

Passo 3

Juntando os resultados obtidos, teremos:

y 2 2 - ln ⁡ y + 1 2 ln ⁡ y 2 + 1 + C

Resposta

y 2 2 - ln ⁡ y + 1 2 ln ⁡ y 2 + 1 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral.int (10)/(( x - 1 ) ( x^2 + 9 )) d x
Calcule a integral.int_0^1 (x)/(x^2 + 4 x + 13) d x
Calcule a integral.int (x^3)/(x^3 + 1) d x
Faça uma substituição para expressar o integrando como uma função racional e então calcule a integral. ∫ x 3 x 2 + 1 3 d x
Faça uma substituição para expressar o integrando como uma função racional e então calcule a integral. ∫ 1 3 1 x x 2 + xd x