Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.9 - Ex. 19
Nos exercícios 11 a 19, calcular o volume do sólido delimitado pelas superfícies dadas.
19. e .
Passo 1
Bora começar?!
Então galera, a primeira coisa a fazer aqui é tentar desenhar:
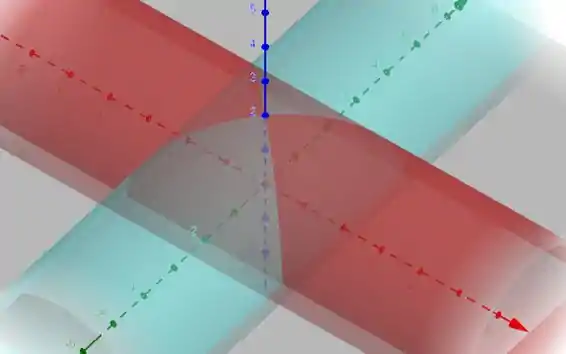
Vamos fazer diferente aqui!
Vamos primeiro isolar o x e, em seguida, o y, tudo bem?
O x vai ser limitado pelo cilindro:
O x será definido por:
Já o y será limitado pelo cilindro:
Então:
Obrigatoriamente:
Que nos dá:
Passo 2
Agora que já sabemos os intervalos de integração:
Resolvendo:
Sendo assim:
Resolvendo a segunda integral:
Aplicando o resultado na última integral:
No intervalo:
O que acharam desta?
Resposta
Exercícios de Livros Relacionados
A função densidade conjunta das variáveis aleatórias X ,Y e Z é f x , y , z = C x y z se 0 ≤ x ≤ 2 , 0 ≤ y ≤ 2 , 0 ≤ z ≤ 2 e f x , y , z = 0 caso contrário.Determine o valor da constante C .Determine
Use a Regra do Ponto Médio para as integrais triplas (Exercício 24) para estimar o valor da integral. Divida B em oito subcaixas de tamanho igual. ∭ B cos x y z d V Onde B = x , y , z | 0 ≤ x ≤ 1,0
Use a Regra do Ponto Médio para as integrais triplas (Exercício 24) para estimar o valor da integral. Divida B em oito subcaixas de tamanho igual. ∭ B x e x y z d V Onde B = x , y , z | 0 ≤ x ≤ 4 , 0
Na Regra do Ponto médio para as Integrais Triplas usamos a soma tripla de Riemann para aproximar a integral tripla sobre uma caixa B, onde f ( x , y , z ) é calculada no centro ( x - , y - , z - ) da
Calcular o volume do tetraedro da Figura 8.32.