Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 51
A função densidade conjunta das variáveis aleatórias e é se , , e caso contrário.
- Determine o valor da constante .
- Determine .
- Determine
Passo 1
Faaala, pessoal!
Nessa questão, a gente vai explorar o conceito de função densidade conjunta.
Ela da pra gente uma função
Para , , , e para qualquer outro ponto.
Essa é uma função que define a probabilidade das variáveis aleatórias caírem em uma região assim:
A questão pede na letra (a) pra descobrirmos quem é essa constante que está na função!
Pra isso vamos usar da propriedade dessas funções que diz:
Já nas letras (b) e (c), precisamos calcular as probabilidades de eventos específicos. Então, vamos calcular a probabilidade pela definição da função densidade conjunta, que vão ser integrais!
Uma observação: nessa questão, vamos usar essa propriedade de integrais triplas:
Ou seja, se o integrando for um produto de funções de cada uma das variáveis, podemos separar a integral como um produto de integrais simples. Mas isso só vale quando os limites de integração são todos constantes!
Passo 2
(a)
Como já vimos, a função densidade conjunta tem que satisfazer
Só que a questão nos disse que pra qualquer vamos de fora da região:
A função vale .
Ou seja, pra cada uma das variáveis, os intervalos de a e de a vão acrescentar em nada na integral... então podemos reescrever essa integral somente na região onde as variáveis estão entre e :
Bom, agora basta integrarmos isso.
Tirando o , que é constante, da integral, ficamos com um produto de funções de , , e :
Então,
Calculando as integrais:
Resolvendo as contas:
Passo 3
(b)
A probabilidade é calculada pela fórmula
Para esse item, nosso é:
Então:
Só que de novo, vamos lembrar que a nossa função vale zero se qualquer uma das integrais estiver fora do intervalo , então podemos tirar os intervalos de até das variáveis:
De novo podemos tirar o da integral e separar num produto de três integrais simples:
Resolvendo:
Resolvendo:
Então:
Passo 4
(c)
Agora vamos de novo usar a fórmula da probabilidade para calcular:
Só que agora nosso é definido por:
Vamos desenhar essa região no . Ela é limitada pelo plano:
E vamos pegar a região só no primeiro octante (), já que fora disso a função vale :
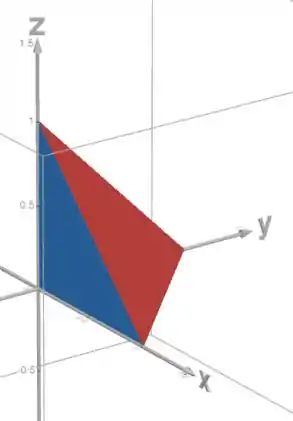
Em vermelho é o plano que limita a região, e em azul a região .
Como esse plano pode ser escrito como
E a região está abaixo desse plano ( é menor que isso) e :
Já para os limites de e vamos olhar a projeção de no plano ():
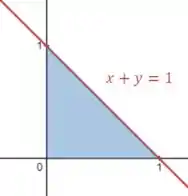
Essa reta vermelha podemos reescrever como:
E como está entre e essa reta:
E o está entre e :
Assim, podemos transformar nossa integral e integral iterada.
Percebe que como os limites de dependem de e , temos que integrar em função de primeiro.
E os limites de dependem de , então, integramos em função de antes de :
Passo 5
Agora vamos calcular essa integral, sempre de dentro pra fora!
Começando em função de , com e constantes:
O pode sair da integral toda, por ser constante. Já o sai das duas primeiras integrais, e o sai só da primeira:
Substituindo os limites de integração:
Podemos tirar o da integral:
Abrindo o quadrado:
Agora integramos em função de , considerando constante:
Passo 6
Por último, pra integrar em função de , vamos fazer uma substituição :
Então:
Esse termo faz os limites de integração inverterem, e colocamos em evidência:
Então:
Tiramos o da integral e finalmente integramos:
Substituindo os limites de integração:
Então:
Resposta
(a)
(b)
(c)