Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 2.5 - Ex. 11a

Nos exercícios de 2 a 15 :

  1. Determine os traços
  2. Determine as seções
  3. Identifique a superfície quadrica
  4. Esboce os gráficos

11.

x 2 + y 2 + z 2 - 2 y - 2 x + 1 = 0

Passo 1

Oii, neste capitulo vamos usar tudo o que sabemos de Geometria Analitica. Vamos arregaçar as mangas e rabiscar bastante no caderno. Vamos lembrar de algumas coisas basicas. Podemos expressar formar geometricas atraves de equações matematicas. E cada equação, mesmo que mude apenas um sinal de + ou – , vai nos dizer um comportamento geometrico diferente. Por exemplo temos essas equações

y = a x 2 → Parábola

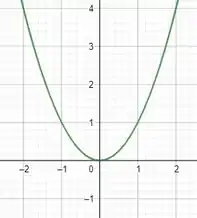
x 2 + y 2 = a 2 → Circulo

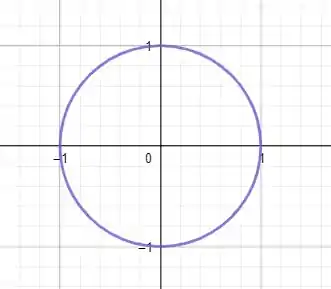
Agora se colocarmos um fator multiplicando x ou y esse circulo vai se achatar ficando oval. Chamamos isso de elipse. Voce pode encontrar essa forma sob os seguintes formatos

a x 2 + b y 2 = c

Ou,

x α 2 + y β 2 = 1

Onde no segundo caso vemos de forma mais clara os raios de x e y. O raio de x será a e o raio de y será b .

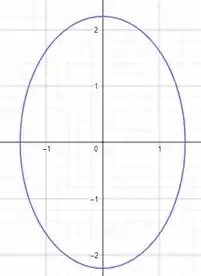
Agora, se trocarmos o sinal da equação geral da elispse, obtemos uma hiperbole. Voce pode encontrar essa forma sob os seguintes formatos

a x 2 - b y 2 = c

Ou,

x α 2 - y β 2 = 1

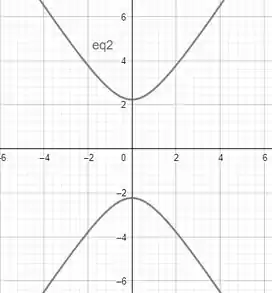
É interessante notar que se botarmos num mesmo plano as equações

x α 2 - y β 2 = 1

e

x α 2 + y β 2 = 1

Vemos o seguinte resultado

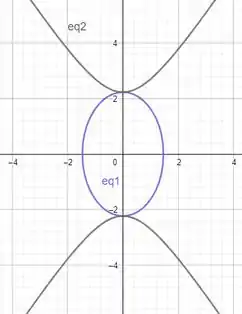
É como se o sinal forçasse a concavidade das curvas virar para dentro ou para fora. Para dentro elas se unem numa elipse e para fora as curvas explodem para infinito dando forma as hiperboles.

Passo 2

Quando o exercício pede traços ele quer que vejamos as imagens dessa função quadrica nos 3 planos coordenados: XY , XZ ,YZ. E com isso a gente conseguir formar imagens mais nítidas de como nossa quadrica deve ser. Vamos cair dentro então. Temos a função

x 2 + y 2 + z 2 - 2 y - 2 x + 1 = 0

Podemos manipular um pouco essa equação e obter o seguinte

x 2 - 2 x + 1 + y 2 - 2 y + z 2 = 0

Vamos completar quadrados para ter uma equação mais limpa

x 2 - 2 x + 1 + y 2 - 2 y + 1 - 1 + z 2 = 0

x - 1 2 + y - 1 2 - 1 + z 2 = 0

x - 1 2 + y - 1 2 + z 2 = 1

Agora sim estamos prontos para ver os planos coordenados!

Passo 3

Plano XY, temos que z = 0

x - 1 2 + y - 1 2 = 1

Que é um círculo de raio 1, com o centro deslocado

Plano XZ, temos que y = 0

x - 1 2 + - 1 2 + z 2 = 1

x - 1 2 + z 2 = 0

A única maneira de dois números positivos, estamos com duas partes elevadas ao quadrado logo temos valores positivos, somados der nulo é se esses números forem 0. Logo

z = 0

x = 1

Estamos com o ponto 1,0 , 0

Agora se formos olhar para o plano YZ , temos que x = 0 . Assim nossa equação fica

- 1 2 + y - 1 2 + z 2 = 1

y - 1 2 + z 2 = 0

Que pelo mesmo motivo do traço anterior, temos que fazer com que cada termo seja nulo, assim :

z = 0

y = 1

O que nos da o seguinte ponto : 0,1 , 0

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

x 2 + y 2 + z 2 - 2 y - 2 x + 1 = 0

Plano XY, temos que z = 0

x - 1 2 + y - 1 2 = 1

Que é um círculo de raio 1, com o centro deslocado

Plano XZ, temos que y = 0

x - 1 2 + z 2 = 0

Estamos com o ponto 1,0 , 0

Agora se formos olhar para o plano YZ , temos que x = 0 . Assim nossa equação fica

y - 1 2 + z 2 = 0

O que nos da o seguinte ponto : 0,1 , 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Identifique a superfície:x^2 - y^2 + z^2 + 2 y + 3 = 0
Determine as seções:x^2 + z^2 - (4)/(9) y^2 = 0
Determine os traços:Ache a equação da superficie de pontos P = ( x , y , z ) cuja distância ao eixo y é 2 3 da distância de P ao plano x z . Identifique a superficie.
Determine as seções:x^2 + y^2 + z^2 - 2 y - 2 x + 1 = 0
Nos exercícios de 2 a 15: c)Identifique a superfície quádrica.15-Escreva a equação da superfície de P = ( x ,y ,z ) tais que a distâncias de P ao ponto ( 0 ,0 ,1 ) é a mesma do que a de P ao plano y =